题目内容
已知函数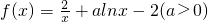 .
.
(1)若对于?x∈(0,+∞)都有f(x)>2(a-1)成立,试求a的取值范围;
(2)记g(x)=f(x)+x-b(b∈R).当a=1时,函数g(x)在区间[e-1,e]上恰有两个零点,求实数b的取值范围.
解:(1)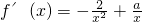 =
= ,由f′(x)>0解得
,由f′(x)>0解得 ,
,
由f′(x)<0得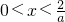
∴f(x)在区间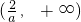 上单调递增,在区间
上单调递增,在区间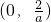 上单调递减
上单调递减
∴当 时,函数f(x)取得最小值
时,函数f(x)取得最小值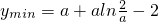
由于对于?x∈(0,+∞)都有f(x)>2(a-1)成立,
所以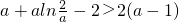
解得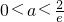 ,故a的取值范围是
,故a的取值范围是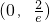
(2)依题意得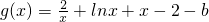 ,则
,则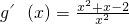
由g′(x)>0解得x>1;由g′(x)<0解得0<x<1
所以g(x)在区间(0,1)上为减函数,在区间(1,+∞)上为增函数.
又因为函数g(x)在区间[e-1,e]上有两个零点,
所以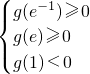
解得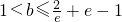 ,
,
所以b的取值范围是 .
.
分析:(1)根据函数的单调区间求出函数的最小值,要使f(x)>2(a-1)恒成立,需使函数的最小值大于2(a-1),从而求得a的取值范围.
(2)利用导数的符号求出单调区间,再根据函数g(x)在区间[e-1,e]上有两个零点,得到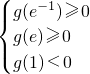 ,解出实数b的取值范围.
,解出实数b的取值范围.
点评:本题考查导数与曲线上某点的切线斜率的关系,利用导数求函数的单调区间以及函数的最值.属于中档题.
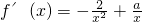 =
= ,由f′(x)>0解得
,由f′(x)>0解得 ,
,由f′(x)<0得
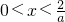
∴f(x)在区间
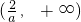 上单调递增,在区间
上单调递增,在区间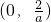 上单调递减
上单调递减∴当
 时,函数f(x)取得最小值
时,函数f(x)取得最小值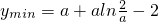
由于对于?x∈(0,+∞)都有f(x)>2(a-1)成立,
所以
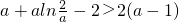
解得
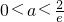 ,故a的取值范围是
,故a的取值范围是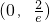
(2)依题意得
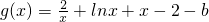 ,则
,则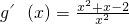
由g′(x)>0解得x>1;由g′(x)<0解得0<x<1
所以g(x)在区间(0,1)上为减函数,在区间(1,+∞)上为增函数.
又因为函数g(x)在区间[e-1,e]上有两个零点,
所以
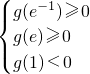
解得
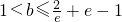 ,
,所以b的取值范围是
 .
.分析:(1)根据函数的单调区间求出函数的最小值,要使f(x)>2(a-1)恒成立,需使函数的最小值大于2(a-1),从而求得a的取值范围.
(2)利用导数的符号求出单调区间,再根据函数g(x)在区间[e-1,e]上有两个零点,得到
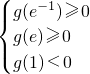 ,解出实数b的取值范围.
,解出实数b的取值范围.点评:本题考查导数与曲线上某点的切线斜率的关系,利用导数求函数的单调区间以及函数的最值.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 上的最大值和最小值;
上的最大值和最小值; .
. .
. 上的最大值和最小值;
上的最大值和最小值; .
. ,
, 有
有 成立,求
成立,求 的取值范围;
的取值范围; ,对于任意的
,对于任意的 都成立,求
都成立,求 。
。 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 恒成立,求实数
恒成立,求实数