题目内容
20.某学科测试中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如表:| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
(Ⅱ)若在(Ⅰ)问中被抽出的答卷中,A,B,C三题答卷得优的份数都是2,从被抽出的A,B,C三题答卷中再各抽出1份,求这3份答卷中恰有1份得优的概率;
(Ⅲ)测试后的统计数据显示,B题的答卷得优的有100份,若以频率作为概率,在(Ⅰ)问中被抽出的选择B题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望EX.
分析 (I)由$\frac{180}{3}$=60可知:每60份试卷抽一份,即可得出;
(II)记事件M:被抽出的A、B、C三种答卷中分别再任取出1份,这3份答卷中恰有1份得优,可知只能C题答案为优,利用相互独立试卷的概率计算公式即可得出;
(Ⅲ)由题意可知,B题答案得优的概率为$\frac{1}{3}$,显然被抽出的B题的答案中得优的份数X的可能取值为0,1,2,3,4,5,且X~B$(5,\frac{1}{3})$.利用P(X=k)=${∁}_{5}^{k}(\frac{1}{3})^{k}(\frac{2}{3})^{5-k}$(k=0,1,2,3,4,5),及其E(X)=np即可得出分布列及其数学期望.
解答 解:(Ⅰ)由题意可得:
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 230 |
| 抽出的答卷数 | 3 | 5 | 2 |
(Ⅱ)记事件M:被抽出的A、B、C三种答卷中分别再任取出1份,这3份答卷中恰有1份得优,可知只能C题答案为优,依题意P(M)=$\frac{1}{3}×\frac{3}{5}×1$=$\frac{1}{5}$.
(Ⅲ)由题意可知,B题答案得优的概率为$\frac{1}{3}$,显然被抽出的B题的答案中得优的份数X的可能取值为0,1,2,3,4,5,且X~B$(5,\frac{1}{3})$.P(X=k)=${∁}_{5}^{k}(\frac{1}{3})^{k}(\frac{2}{3})^{5-k}$(k=0,1,2,3,4,5),可得P(X=0)=$\frac{32}{243}$,P(X=1)=$\frac{80}{243}$,P(X=2)=$\frac{80}{243}$,P(X=3)=$\frac{40}{243}$,P(X=4)=$\frac{10}{243}$,P(X=0)=$\frac{1}{243}$,
随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{32}{243}$ | $\frac{80}{243}$ | $\frac{80}{243}$ | $\frac{40}{243}$ | $\frac{10}{243}$ | $\frac{1}{243}$ |
点评 本题考查了随机变量的二项分布列及其数学期望、分层抽样、相互独立事件的概率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$.
用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$.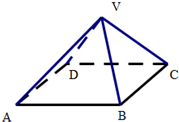 如图:正四棱锥V-ABCD中,高为2,底面ABCD是边长为4的正方形,则二面角V-AB-C的平面角为45°.
如图:正四棱锥V-ABCD中,高为2,底面ABCD是边长为4的正方形,则二面角V-AB-C的平面角为45°.