题目内容
12.已知数列{an}满足an≠0,a1=$\frac{1}{3}$,an-1-an=2an•an-1(n≥2,n∈N*),则an=$\frac{1}{2n+1}$,a1a2+a2a3+…+a99a100=$\frac{11}{67}$.分析 通过对an-1-an=2an•an-1(n≥2,n∈N*)变形可得数列{$\frac{1}{{a}_{n}}$}是以3为首项、2为公差的等差数列,计算可得通项,再利用拆项法、并项相加即得结论.
解答 解:∵an-1-an=2an•an-1(n≥2,n∈N*),an≠0,
∴2=$\frac{{a}_{n-1}-{a}_{n}}{{a}_{n}•{a}_{n-1}}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$,
又∵a1=$\frac{1}{3}$,∴$\frac{1}{{a}_{1}}$=3,
∴数列{$\frac{1}{{a}_{n}}$}是以3为首项、2为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=3+2(n-1)=2n+1,
∴an=$\frac{1}{2n+1}$;
∴an•an+1=$\frac{1}{2n+1}•\frac{1}{2n+3}$=$\frac{1}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),
∴a1a2+a2a3+…+a99a100=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{197}$-$\frac{1}{199}$+$\frac{1}{199}$-$\frac{1}{201}$)
=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{201}$)=$\frac{11}{67}$,
故答案为:$\frac{1}{2n+1}$,$\frac{11}{67}$.
点评 本题考查求数列的通项,对表达式的灵活变形和并项相加法是解决本题的关键,属于中档题.

 阅读快车系列答案
阅读快车系列答案| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
(Ⅱ)若在(Ⅰ)问中被抽出的答卷中,A,B,C三题答卷得优的份数都是2,从被抽出的A,B,C三题答卷中再各抽出1份,求这3份答卷中恰有1份得优的概率;
(Ⅲ)测试后的统计数据显示,B题的答卷得优的有100份,若以频率作为概率,在(Ⅰ)问中被抽出的选择B题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望EX.

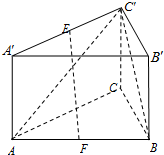 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.