题目内容
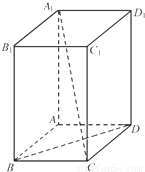
在长方体BCD-A1B1C1D1中,E、F分别是棱BC,CC1上的点,CF=AB=2CE,AB:AD:AA1=1:2:4
(1)求异面直线EF与A1D所成角的余弦值;
(2)求二面角A1-ED-F的正弦值.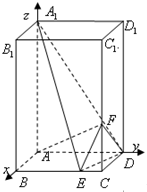
(1)求异面直线EF与A1D所成角的余弦值;
(2)求二面角A1-ED-F的正弦值.

如图所示,建立空间直角坐标系,点A为坐标原点,设AB=1,依题意得D(0,2,0),F(1,2,1),A1(0,0,4),E(1,
,0),
(1)易得
=(0,
,1),
=(0,2,-4),于是cos<
,
>=
=-
,

所以异面直线EF与A1D所成角的余弦值为
.
(2)设平面EFD的法向量
=(x,y,z),则
•
=
y+z=0,且
•
=-x+
y=0,
不妨令x=1,可得
=(1,2,-1),
设平面A1ED的法向量
=(m,n,p)则
•
=-m+
n=0且
•
=-2n+4p=0,
取p=1,则n=2,m=1,则
=(1,2,1),
于是cos<
,
>=
=
,从而sin<
,
>=
,
所以二面角A1-ED-F的正弦值为
.
| 3 |
| 2 |
(1)易得
| EF |
| 1 |
| 2 |
| A1D |
| EF |
| A1D |
| ||||
|
|
| 3 |
| 5 |

所以异面直线EF与A1D所成角的余弦值为
| 3 |
| 5 |
(2)设平面EFD的法向量
| n |
| n |
| EF |
| 1 |
| 2 |
| n |
| ED |
| 1 |
| 2 |
不妨令x=1,可得
| n |
设平面A1ED的法向量
| m |
| m |
| ED |
| 1 |
| 2 |
| m |
| DA1 |
取p=1,则n=2,m=1,则
| m |
于是cos<
| n |
| m |
| ||||
|
|
| 2 |
| 3 |
| n |
| m |
| ||
| 3 |
所以二面角A1-ED-F的正弦值为
| ||
| 3 |

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
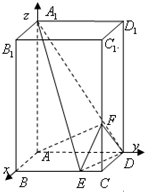 在长方体BCD-A1B1C1D1中,E、F分别是棱BC,CC1上的点,CF=AB=2CE,AB:AD:AA1=1:2:4
在长方体BCD-A1B1C1D1中,E、F分别是棱BC,CC1上的点,CF=AB=2CE,AB:AD:AA1=1:2:4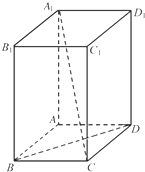 (2007•广州一模)如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结A1C、BD.
(2007•广州一模)如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结A1C、BD.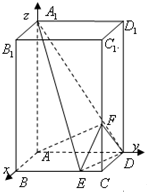 在长方体BCD-A1B1C1D1中,E、F分别是棱BC,CC1上的点,CF=AB=2CE,AB:AD:AA1=1:2:4
在长方体BCD-A1B1C1D1中,E、F分别是棱BC,CC1上的点,CF=AB=2CE,AB:AD:AA1=1:2:4