题目内容
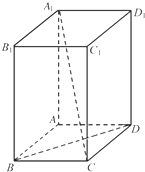 (2007•广州一模)如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结A1C、BD.
(2007•广州一模)如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结A1C、BD.(Ⅰ)求证:A1C⊥BD;
(Ⅱ)求三棱锥A1-BCD的体积.
分析:(Ⅰ)利用线面垂直的性质先证明BD⊥平面A1AC,然后再证:A1C⊥BD;
(Ⅱ)根据锥体的体积公式求体积即可.
(Ⅱ)根据锥体的体积公式求体积即可.
解答:解: (Ⅰ)证明:连AC.
(Ⅰ)证明:连AC.
∵AB=BC,
∴BD⊥AC. …(2分)
∵A1A⊥底面ABCD,
∴BD⊥A1A. …(4分)
∵A1A?平面A1AC,AC?平面A1AC,A1A∩AC=A,
∴BD⊥平面A1AC. …(6分)
∴BD⊥A1C. …(8分)
(Ⅱ)解:∵A1A⊥平面BCD,所以A1A是锥体的高,
∴VA1-BCD=
S△BCD•AA1=
×
×1×1×2=
.…(14分)
 (Ⅰ)证明:连AC.
(Ⅰ)证明:连AC.∵AB=BC,
∴BD⊥AC. …(2分)
∵A1A⊥底面ABCD,
∴BD⊥A1A. …(4分)
∵A1A?平面A1AC,AC?平面A1AC,A1A∩AC=A,
∴BD⊥平面A1AC. …(6分)
∴BD⊥A1C. …(8分)
(Ⅱ)解:∵A1A⊥平面BCD,所以A1A是锥体的高,
∴VA1-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题主要考查线面垂直的性质以及应用,锥体的体积公式.

练习册系列答案
相关题目
 (2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.
(2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.