Question

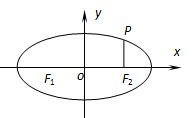（2009•金山区二模）已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0），F₁、F₂分别为其左、右焦点，点P（

2

，1）在椭圆C上，且PF₂垂直于x轴．
（1）求椭圆C的方程；（2）设坐标平面上有两点A（-5，-4）、B（3，0），过点P作直线l，交线段AB于点D，并且直线l将△PAB分成的两部分图形的面积之比为5：3，求D点的坐标．

Answer 1

分析：（1）根据点P（

2

，1）在椭圆C上，且PF₂垂直于x轴，可知右焦点坐标，从而可求PF₁的长，故可求椭圆C的方程；
（2）根据直线l将△PAB分成的两部分图形的面积之比为5：3，可得D分

AB

所成的比，利用定比分点坐标公式可求D点的坐标．

解答：解：（1）因为点P（

2

，1）在椭圆C上，且PF₂垂直于x轴，
所以F₂（

2

，0），即c=

2

，…（1分）
又PF₂=1，所以PF₁=3，…（3分）
所以2a=4，a=2，…（4分）
所以b²=a²-c²=2
所以，所求椭圆方程为

x2

4

+

y2

2

=1…（6分）
（2）过点P作直线l，交线段AB于点D，则其坐标可设为D（x，y），…（7分）
又直线l将△PAB分成的两部分图形的面积之比为5：3，
即有：点D在线段AB上，且AD：DB=5：3或AD：DB=3：5
因为A（-5，-4）、B（3，0），设D分

AB

所成的比为λ，λ=

5

3

或λ=

3

5

…（9分）
所以x=

-5+ 5 3 ×3

1+ 5 3

=0，y=

-4+ 5 3 ×0

1+ 5 3

=-

3

2

或x=

-5+ 3 5 ×3

1+ 3 5

=2，y=

-4+ 3 5 ×0

1+ 3 5

=-

5

2

，
所以点D的坐标为（0，-

3

2

）或（-2，-

5

2

）…（12分）

点评：本题的考点是直线与圆锥曲线的综合问题，主要考查椭圆的标准方程，考查线段的定比分点坐标公式，有一定的综合性