题目内容
已知函数 (a∈R).
(a∈R).
(1)若a=3,试确定函数f(x)的单调区间;
(2)若函数f(x)在其图象上任意一点(x0,f(x0))处切线的斜率都小于2a2,求实数a的取值范围.
(3)若?x∈[0,2],f(x)<0,求a的取值范围.
解:(1)∵函数 (a∈R),∴f′(x)=-x2+2x+a.
(a∈R),∴f′(x)=-x2+2x+a.
当a=3时,f′(x)=-x2+2x+3=-(x+1)(x-3).
当x∈(-∞,-1)或(3,+∞)时,f′(x)<0;当x∈(-1,3)时,f′(x)>0.
∴函数f(x)在区间(-∞,-1)或(3,+∞)上单调递减;在区间(-1,3)上单调递增.
(2)∵f′(x)=-x2+2x+a,∴函数f(x)在其图象上任意一点(x0,f(x0))处切线的斜率为 ,
,
由题意可知:对任意的实数x0, 恒成立.
恒成立.
即 对任意实数x0恒成立?
对任意实数x0恒成立? ,x∈R.
,x∈R.
令φ(x0)= ,则φ(x0)=
,则φ(x0)= ≤1,∴
≤1,∴ =1.
=1.
∴2a2-a>1,
解得a>1,或a< .
.
∴a的取值范围是(-∞, )∪(1,+∞).
)∪(1,+∞).
(3)①当x=0时,f(0)=0,∵0<0不可能,此时不存在a满足要求;
②当x∈(0,2]时,若?x∈(0,2],f(x)<0,??x∈(0,2], .
.
∵φ(x)= =
= ,∴φ(x)在区间(0,
,∴φ(x)在区间(0, )单调递减,在区间
)单调递减,在区间 单调递增,但是φ(0)=0>φ(2),故φ(x)在区间(0,2]上无最大值.
单调递增,但是φ(0)=0>φ(2),故φ(x)在区间(0,2]上无最大值.
经验证a=0 时适合题意.
∴a≤0.
分析:(1)先求导,看其f′(x)在某区间上是大于0、还是小于0.即可判断出单调区间.
(2)已知问题? 对任意实数x0恒成立?
对任意实数x0恒成立? ,x∈R.解出即可.
,x∈R.解出即可.
(3)对x分x=0 与x∈(0,2]讨论,对x∈(0,2]可转化为:当x∈(0,2]时,若?x∈(0,2],f(x)<0,??x∈(0,2], .求出即可.
.求出即可.
点评:本题综合考查了利用导数求单调区间、恒成立即存在性问题,转化思想是解决问题的关键.
 (a∈R),∴f′(x)=-x2+2x+a.
(a∈R),∴f′(x)=-x2+2x+a.当a=3时,f′(x)=-x2+2x+3=-(x+1)(x-3).
当x∈(-∞,-1)或(3,+∞)时,f′(x)<0;当x∈(-1,3)时,f′(x)>0.
∴函数f(x)在区间(-∞,-1)或(3,+∞)上单调递减;在区间(-1,3)上单调递增.
(2)∵f′(x)=-x2+2x+a,∴函数f(x)在其图象上任意一点(x0,f(x0))处切线的斜率为
 ,
,由题意可知:对任意的实数x0,
 恒成立.
恒成立.即
 对任意实数x0恒成立?
对任意实数x0恒成立? ,x∈R.
,x∈R.令φ(x0)=
 ,则φ(x0)=
,则φ(x0)= ≤1,∴
≤1,∴ =1.
=1.∴2a2-a>1,
解得a>1,或a<
 .
.∴a的取值范围是(-∞,
 )∪(1,+∞).
)∪(1,+∞).(3)①当x=0时,f(0)=0,∵0<0不可能,此时不存在a满足要求;
②当x∈(0,2]时,若?x∈(0,2],f(x)<0,??x∈(0,2],
 .
.∵φ(x)=
 =
= ,∴φ(x)在区间(0,
,∴φ(x)在区间(0, )单调递减,在区间
)单调递减,在区间 单调递增,但是φ(0)=0>φ(2),故φ(x)在区间(0,2]上无最大值.
单调递增,但是φ(0)=0>φ(2),故φ(x)在区间(0,2]上无最大值.经验证a=0 时适合题意.
∴a≤0.
分析:(1)先求导,看其f′(x)在某区间上是大于0、还是小于0.即可判断出单调区间.
(2)已知问题?
 对任意实数x0恒成立?
对任意实数x0恒成立? ,x∈R.解出即可.
,x∈R.解出即可.(3)对x分x=0 与x∈(0,2]讨论,对x∈(0,2]可转化为:当x∈(0,2]时,若?x∈(0,2],f(x)<0,??x∈(0,2],
 .求出即可.
.求出即可.点评:本题综合考查了利用导数求单调区间、恒成立即存在性问题,转化思想是解决问题的关键.

练习册系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).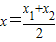 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.