题目内容
已知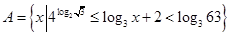
,函数
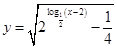的定义域为
(1)求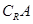
；
(2)求
。
(1)
(2)
解析试题分析：求解对数不等式化简集合A，求含有根式对数函数的定义域得到集合B，然后直接利用补集交集概念求解;其中
恒等变形应用比较灵活,在求集合A,B中都有用到;本题易忘记真数范围.
试题解析：
故
(2)要使函数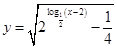有意义则
可化为
即
故
考点：补集、交集及其运算；其他不等式的解法,根式及对数性质．
练习册系列答案
相关题目
题目内容
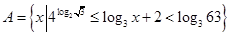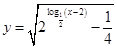已知,函数的定义域为
(1)求；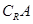
(2)求。
(1)(2)
解析试题分析：求解对数不等式化简集合A，求含有根式对数函数的定义域得到集合B，然后直接利用补集交集概念求解;其中恒等变形应用比较灵活,在求集合A,B中都有用到;本题易忘记真数范围.
试题解析：
故
(2)要使函数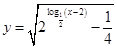有意义则
可化为即
故
考点：补集、交集及其运算；其他不等式的解法,根式及对数性质．
=1,m≠0，|m|≠1}满足A∩B≠
,A∩C=
与
分别是函数
的定义域与值域.
；
时，求实数
的取值范围．
，B＝
，求实数
的取值范围. 
，
．
，求实数
的值；
，求实数
，集合
.
,求
;
,求
的取值范围.
，集合
.
,求
;
,求
的取值范围.