题目内容
已知向量 =(sinx,-cosx),
=(sinx,-cosx), =(cosθ,-sinθ),其中0<θ<π.函数f(x)=
=(cosθ,-sinθ),其中0<θ<π.函数f(x)= 在x=π处取最小值.
在x=π处取最小值.
(Ⅰ)求θ的值;
(Ⅱ)设A,B,C为△ABC的三个内角,若sinB=2sinA, ,求A.
,求A.
解:(Ⅰ)∵f(x)= =sinxcosθ+cosxsinθ=sin(x+θ)
=sinxcosθ+cosxsinθ=sin(x+θ)
又∵函数f(x)在x=π处取最小值,∴sin(π+θ)=-1,即 sinθ=-1
又0<θ<π,∴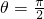 …(5分)∴
…(5分)∴
(Ⅱ)法一:∵ ,∴
,∴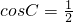 ∵0<C<π,∴
∵0<C<π,∴ .
.
∵A+B+C=π,∴
代入sinB=2sinA中,∴ ,∴
,∴ ,
,
∴ ,
,
∵0<A<π,∴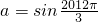 .
.
(Ⅱ)法二:∵ ,∴
,∴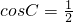 ∵0<C<π,∴
∵0<C<π,∴ .
.
∵sinB=2sinA,由正弦定理有b=2a.
又由余弦定理得
∴a2+c2=b2,∴
∵A+B+C=π,∴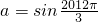 .
.
分析:(Ⅰ)通过向量的数量积以及两角和的正弦函数,化简函数为一个角的一个三角函数的形式,通过x=π处取最小值求θ的值;
(Ⅱ)发一:通过 ,求出C的值,利用三角形的内角和与sinB=2sinA,通过三角代换直接求A.
,求出C的值,利用三角形的内角和与sinB=2sinA,通过三角代换直接求A.
法二:通过 ,求出C的值,利用正弦定理和余弦定理,求出B,然后求出A.
,求出C的值,利用正弦定理和余弦定理,求出B,然后求出A.
点评:本题通过向量的数量积,考查三角函数的基本公式的应用,正弦定理与余弦定理的应用,考查计算能力,好题,常考题型.
 =sinxcosθ+cosxsinθ=sin(x+θ)
=sinxcosθ+cosxsinθ=sin(x+θ)又∵函数f(x)在x=π处取最小值,∴sin(π+θ)=-1,即 sinθ=-1
又0<θ<π,∴
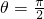 …(5分)∴
…(5分)∴
(Ⅱ)法一:∵
 ,∴
,∴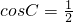 ∵0<C<π,∴
∵0<C<π,∴ .
. ∵A+B+C=π,∴

代入sinB=2sinA中,∴
 ,∴
,∴ ,
,∴
 ,
,∵0<A<π,∴
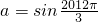 .
. (Ⅱ)法二:∵
 ,∴
,∴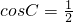 ∵0<C<π,∴
∵0<C<π,∴ .
. ∵sinB=2sinA,由正弦定理有b=2a.
又由余弦定理得

∴a2+c2=b2,∴

∵A+B+C=π,∴
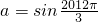 .
. 分析:(Ⅰ)通过向量的数量积以及两角和的正弦函数,化简函数为一个角的一个三角函数的形式,通过x=π处取最小值求θ的值;
(Ⅱ)发一:通过
 ,求出C的值,利用三角形的内角和与sinB=2sinA,通过三角代换直接求A.
,求出C的值,利用三角形的内角和与sinB=2sinA,通过三角代换直接求A.法二:通过
 ,求出C的值,利用正弦定理和余弦定理,求出B,然后求出A.
,求出C的值,利用正弦定理和余弦定理,求出B,然后求出A.点评:本题通过向量的数量积,考查三角函数的基本公式的应用,正弦定理与余弦定理的应用,考查计算能力,好题,常考题型.

练习册系列答案
相关题目
已知向量
=(sinx,cosx),向量
=(1,
),则|
+
|的最大值为( )
| a |
| b |
| 3 |
| a |
| b |
| A、3 | ||
B、
| ||
| C、1 | ||
| D、9 |