Question

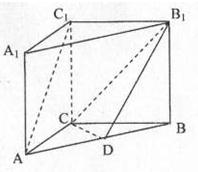如图，在直三棱柱ABC-A₁B₁C₁中，AC=3，BC=4，AB=5，AA₁=4，点D是AB中点．
（1）求证：AC₁∥平面CDB₁；
（2）求异面直线AC₁与B₁C所成角的余弦值；
（3）求二面角B-AC₁-C的正切值．

Answer 1

分析：（1）连接C₁B交CB₁于O点，要证AC₁∥平面CDB₁，只需证明AC₁平行平面CDB₁内的直线DO即可．
（2）由（1）知DO∥AC₁，∠COD就是异面直线AC₁与B₁C所成的角．利用余弦定理求异面直线AC₁与B₁C所成角的余弦值；
（3）在侧面ACC₁A₁内过C作CE⊥AC₁于E，连接BE，说明∠BEC就是二面角B-AC₁-C的平面角，然后求二面角B-AC₁-C的正切值．

解答：解：（1）证明：连接C₁B交CB₁于O点，
由已知四边形BCC₁B₁为矩形，
∴O为C₁B的中点，又D为AB的中点，
连接DO，则DO∥AC₁，
而AC₁?面B₁CD，DO?面B₁CD，
∴AC₁∥面CDB₁．（5分）
（2）解：由（1）知DO∥AC₁，
∴∠COD就是异面直线AC₁与B₁C所成的角．
依题设知：CD=

1

2

AB=

5

2

，CO=

1

2

CB1=2

2

，DO=

1

2

AC1=

5

2

，
∴Cos∠COD=

CO2+DO2-CD2

2•CO•DO

=

8+ 25 4 - 25 4

2•2 2 • 5 2

=

2 2

5

即异面直线AC₁与B₁C所成角的余弦值为

2 2

5

．（9分）
（3）解：依题设BC⊥侧面ACC₁A₁，则在侧面ACC₁A₁内过C作CE⊥AC₁于E，连接BE，由AC₁⊥面BCE知AC₁⊥BE，∴∠BEC就是二面角B-AC₁-C的平面角．在Rt△BCE中，BC=4，CE=

3×4

5

，∴tan∠BEC=

BC

CE

=

5

3

，即二面角B-AC₁-C的正切值为

5

3

．

点评：本题考查直线与平面的垂直的判定，二面角的求法，异面直线所成的角，考查空间想象能力，逻辑思维能力，是中档题．