题目内容
已知函数
是奇函数.
(1)求
的值;
(2)判断函数
的单调性,并用定义证明;
(3)求函数的值域.
是奇函数.(1)求
的值; (2)判断函数
的单调性,并用定义证明;(3)求函数的值域.
（1）1
（2）略
（3）（-1,1）
（1）解：f(x)的定义域是R，且为奇函数 ∴f(0)=0,∴a=1
（2）由（1）知：
，所以f(x)为增函数
证明：任取
，且
＜
∵＜ ∴
＜
，∴
＜0即
∴f(x)是R上的增函数
（3）令
,则
,∵
，∴
，∴-1＜y＜1
所以函数f(x)的值域是（-1,1）
（2）由（1）知：
，所以f(x)为增函数证明：任取
，且＜∵
＜ ∴＜，∴＜0即∴f(x)是R上的增函数
（3）令
,则,∵，∴，∴-1＜y＜1所以函数f(x)的值域是（-1,1）
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
是偶函数，它在
上是增函数.若
则
的取值范围是（ ）
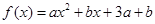是偶函数，且定义域为
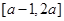，则
_______
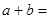为实数，函数
. 
时，判断函数
的奇偶性； 
的最小值；
是奇函数，则
★ 
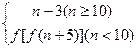，其中n∈N，则f(8)等于 
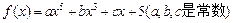，且
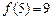，则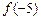
的值为 ▲ ．
是定义在
上的偶函数，当
时，
，则当
时，