题目内容
已知曲线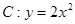 ,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是
,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是
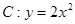 ,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是
,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是 | A.(-∞,10) | B.(10,+∞) | C.(-∞,4) | D.(4,+∞) |
A
分析:先看视线最高时为抛物线切线,而且为右上方向,设出切线的方程与抛物线方程联立消去y,根据判别式等于0求得k的值,进而求得切线的方程,把x=3代入即可求得y的值,B点只要在此切线下面都满足题意,进而求得a的范围.
解答:解:视线最高时为抛物线切线,而且为右上方向
设切线y=kx-2(k>0)
与抛物线方程联立得2x2-kx+2=0
△=k2-16=0
k=4(负的舍去)
∴切线为y=4x-2
取x=3得y=10
B点只要在此切线下面都满足题意
∴a<10
故选A.
解答:解:视线最高时为抛物线切线,而且为右上方向
设切线y=kx-2(k>0)
与抛物线方程联立得2x2-kx+2=0
△=k2-16=0
k=4(负的舍去)
∴切线为y=4x-2
取x=3得y=10
B点只要在此切线下面都满足题意
∴a<10
故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 x2-
x2- x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)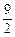 )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;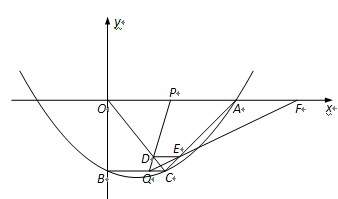
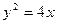 ,过
,过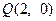 作直线
作直线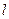 .
.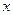 轴不垂直,交抛物线于A、B两点,是否存在
轴不垂直,交抛物线于A、B两点,是否存在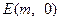 ,使得
,使得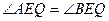 ?若存在,求出m的值;若不存在,请说
?若存在,求出m的值;若不存在,请说 明理由?
明理由?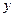 轴和
轴和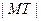 为定值,试证之;
为定值,试证之;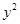 =2x的焦点为F,过点M(
=2x的焦点为F,过点M(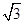 ,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,
,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,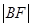 =2,则
=2,则
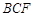 与
与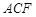 的面积之比
的面积之比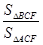 =( )
=( )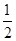
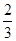
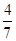
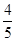
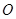 和点
和点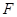 分别是抛物线
分别是抛物线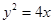 的顶点和焦点,点
的顶点和焦点,点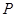 为抛物线上的任意一点,则
为抛物线上的任意一点,则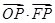 的取值范围为 ( *** )
的取值范围为 ( *** )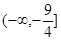
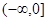
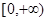
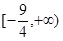
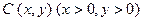 在抛物线
在抛物线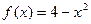 上(如图), 过
上(如图), 过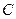 作
作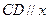 轴交抛物线于另一点
轴交抛物线于另一点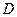 ,设抛物线与
,设抛物线与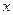 轴相交于
轴相交于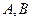 两点,试求
两点,试求 的面积最大,并求出面积的最大值.
的面积最大,并求出面积的最大值.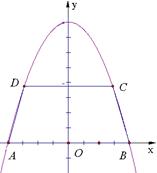
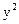 =–x与直线y="k(x" + 1)相交于A、B两点,则△AOB的形状是
=–x与直线y="k(x" + 1)相交于A、B两点,则△AOB的形状是 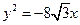 有共同焦点,且一条渐近线方程是
有共同焦点,且一条渐近线方程是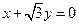 的双曲线的方程是 .
的双曲线的方程是 .