题目内容
已知关于x的不等式
x2+bx+c＜0（b＞0）的解集为R，则T=
的最小值为（ ）
| 1 |
| a |
| 5+2ab+4ac |
| ab+1 |
分析：从二次函数的二次项系数及判别式限制，得到a，b，c满足的不等关系；利用基本不等式求出最小值．
解答：解：∵一元二次不等式
x2+bx+c＜0的解集为R，
∴
，即
．
∵b＞0＞a，∴b-a＞0，
由于b2＜
，则得c＜
，
则T=
＞
=
=(ab+1)+
≥2
=4
当且仅当(ab+1)=
，即ab=-3时，取等号
故答案为：D
| 1 |
| a |
∴
|
|
∵b＞0＞a，∴b-a＞0，
由于b2＜
| 4c |
| a |
| ab2 |
| 4 |
则T=
| 5+2ab+4ac |
| ab+1 |
| 5+2ab+a2b2 |
| ab+1 |
| (ab+1)2+4 |
| ab+1 |
=(ab+1)+
| 4 |
| ab+1 |
(ab+1)•
|
当且仅当(ab+1)=
| 1 |
| ab+1 |
故答案为：D
点评：主要考查了二次函数的恒成立问题．二次函数的恒成立问题分两类，一是大于0恒成立须满足开口向上，且判别式小于0，二是小于0恒成立须满足开口向下，且判别式小于0．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
a＜－1，或a＞2)．
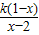+1＜0的解集为空集，求实数k的取值或取值范围．