题目内容
给出下列命题:
(1)已知事件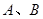 是互斥事件,若
是互斥事件,若 ,则
,则 ;
;
(2)已知事件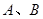 是互相独立事件,若
是互相独立事件,若 ,则
,则 (
( 表示事件
表示事件 的对立事件);
的对立事件);
(3) 的二项展开式中,共有4个有理项.
的二项展开式中,共有4个有理项.
则其中真命题的序号是( )
| A.(1)、(2). | B.(1)、(3). | C.(2)、(3). | D.(1)、(2)、(3). |
D
解析试题分析:对于(1),因为 ,
, 互斥,所以
互斥,所以 ,正确,对于(2)由于
,正确,对于(2)由于 互相独立,所以
互相独立,所以 ,正确,对于(3)其展开式的通项公式为
,正确,对于(3)其展开式的通项公式为 ,
, 要为有理项,则
要为有理项,则 必须为整数,则
必须为整数,则 是6的整数倍,由此
是6的整数倍,由此 共4个数,即展开式中只有4个有理项,正确.选D.
共4个数,即展开式中只有4个有理项,正确.选D.
考点:互斥事件的概率,互相独立事件的概率,二项展开式的通项公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若(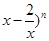 的展开式中第2项与第4项的二项式系数相等,则直线y=nx与曲线y=x2围成的封闭区域面积为( )
的展开式中第2项与第4项的二项式系数相等,则直线y=nx与曲线y=x2围成的封闭区域面积为( )
A.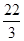 | B.12 | C.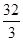 | D.36 |
将6名男生、4名女生分成两组,每组5人,参加两项不同的活动,每组3名男生和2名女生,则不同的分配方法有( )
| A.240种 | B.120种 | C.60种 | D.180种 |
如果某年年份的各位数字之和为7,我们称该年为“七巧年”.例如,今年年份2014
的各位数字之和为7,所以今年恰为“七巧年”.那么从2000年到2999年中“七巧年”共有( )
| A.24个 | B.21个 | C.19个 | D.18个 |
二项式 展开式中的常数项是( )
展开式中的常数项是( )
| A.第7项 | B.第8项 | C.第9项 | D.第10项 |
从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为a,b,共可得到lga-lgb的不同值的个数是( )
| A.9 |
| B.10 |
| C.18 |
| D.20 |
8名学生和2位老师站成一排合影,2位老师不相邻的排法种数为( )
A.  |
B.  |
C.  |
D.  |
在 的展开式中,
的展开式中, 的系数是( )
的系数是( )
| A.-297 | B.-252 | C.297 | D.207 |
使 n(n∈N*)的展开式中含有常数项的最小的n为( )
n(n∈N*)的展开式中含有常数项的最小的n为( )
| A.4 | B.5 |
| C.6 | D.7 |