题目内容
已知函数![]() , 其中
, 其中![]() 且
且![]()
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)设函数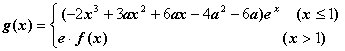 (e是自然对数的底数),是否存在a,使g(x)在[a,-a]上是减函数?若存在,求a的取值范围;若不存在,请说明理由.
(e是自然对数的底数),是否存在a,使g(x)在[a,-a]上是减函数?若存在,求a的取值范围;若不存在,请说明理由.
(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]()
(1)若-1<a<0,则当0<x<-a时,![]() ;当-a <x<1时,
;当-a <x<1时,![]() ;当x>1时,
;当x>1时,![]() .故
.故![]() 分别在
分别在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)若a<-1,仿(1)可得![]() 分别在
分别在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)存在a,使g(x)在[a,-a]上是减函数.
事实上,设![]() ,则
,则
![]() ,再设
,再设![]() ,则当g(x)在[a,-a]上单调递减时,h(x)必在[a,0]上单调递,所以
,则当g(x)在[a,-a]上单调递减时,h(x)必在[a,0]上单调递,所以![]() ,由于
,由于![]() ,因此
,因此![]() ,而
,而![]() ,所以
,所以![]() ,此时,显然有g(x)在[a,-a]上为减函数,当且仅当
,此时,显然有g(x)在[a,-a]上为减函数,当且仅当![]() 在[1,-a]上为减函数,h(x)在[a,1上为减函数,且
在[1,-a]上为减函数,h(x)在[a,1上为减函数,且![]() ,由(Ⅰ)知,当a<-2时,
,由(Ⅰ)知,当a<-2时,![]() 在
在![]() 上为减函数 ①
上为减函数 ①
又![]() ②
②
不难知道,![]()
因![]() ,令
,令![]() ,则x=a或x=-2,而
,则x=a或x=-2,而![]()
于是 (1)当a<-2时,若a <x<-2,则![]() ,若-2 <x<1,则
,若-2 <x<1,则![]() ,因而
,因而![]() 分别在
分别在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)当a=-2时, ![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
综合(1)(2)知,当![]() 时,
时,![]() 在
在![]() 上的最大值为
上的最大值为![]() ,所以,
,所以,![]() ③
③
又对![]() ,只有当a=-2时在x=-2取得,亦即
,只有当a=-2时在x=-2取得,亦即![]() 只有当a=-2时在x=-2取得.
只有当a=-2时在x=-2取得.
因此,当![]() 时,h(x)在[a,1上为减函数,从而由①,②,③知
时,h(x)在[a,1上为减函数,从而由①,②,③知 ![]()
综上所述,存在a,使g(x)在[a,-a]上是减函数,且a的取值范围为![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
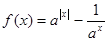 (其中
(其中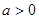 且
且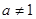 ,
,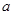 为实常数).
为实常数).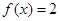 ,求
,求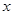 的值(用
的值(用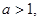 且
且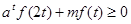 对于
对于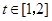 恒成立,求实数m的取值范围(用
恒成立,求实数m的取值范围(用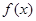 =
=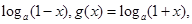 其中
其中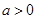 且
且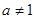 。
。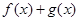 的定义域;
的定义域;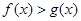 ,求
,求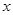 的取值范围。
的取值范围。