题目内容
如图,椭圆C:![]() 焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线y=
焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线y=![]() x上一点P.
x上一点P.

(1)求椭圆C及抛物线C1、C2的方程;
(2)若动直线l与直线OP垂直,且与椭圆C交于不同两点M、N,已知点Q(-![]() ,0),求
,0),求![]() 的最小值.
的最小值.
答案:
解析:
解析:
|
解:(Ⅰ)由题意,A( 故抛物线C1的方程可设为 由 得 所以椭圆C: (Ⅱ)由(Ⅰ)知,直线OP的斜率为 设直线 由 因为动直线 解得 设M( 因为 所以 因为 其最小值等于 |

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目

 ,整理得
,整理得 焦点在
焦点在 轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线 上一点P.
上一点P.
 与直线OP垂直,且与椭圆C交于不同两点M、N,已知点Q(
与直线OP垂直,且与椭圆C交于不同两点M、N,已知点Q( ,0),求
,0),求 的最小值.
的最小值. 焦点在x轴上,左、右顶点分别为A1,A,上顶点为B,抛物线C1,C2分别以A,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
焦点在x轴上,左、右顶点分别为A1,A,上顶点为B,抛物线C1,C2分别以A,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线 上一点P。
上一点P。
 ,求
,求 的最小值。
的最小值。 焦点在x轴上,左、右顶点分别为A1、A,上顶点为B,抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O.C1与C2相交于直线
焦点在x轴上,左、右顶点分别为A1、A,上顶点为B,抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O.C1与C2相交于直线 上一点P.
上一点P.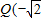 ,0),求
,0),求 的最小值.
的最小值.
 焦点在x轴上,左、右顶点分别为A1、A,上顶点为B,抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O.C1与C2相交于直线
焦点在x轴上,左、右顶点分别为A1、A,上顶点为B,抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O.C1与C2相交于直线 上一点P.
上一点P. ,0),求
,0),求 的最小值.
的最小值.
 焦点在x轴上,左、右顶点分别为A1、A,上顶点为B,抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O.C1与C2相交于直线
焦点在x轴上,左、右顶点分别为A1、A,上顶点为B,抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O.C1与C2相交于直线 上一点P.
上一点P. ,0),求
,0),求 的最小值.
的最小值.