题目内容
不论k为何值,直线(2k-1)x-(k-2)y-(k+4)=0恒过的一个定点是
- A.(0,0)
- B.(2,3)
- C.(3,2)
- D.(-2,3)
B
分析:方法1:不论k为何值直线恒过定点,即跟参数k无关,原直线方程可整理为(2x-y-1)k-(x-2y+4)=0,k的系数为0,解方程组即可.
方法2:因为是选择题,跟k无关,不妨取两个特殊值,确定两条直线求交点即可.
解答:方法1:直线方程(2k-1)x-(k-2)y-(k+4)=0
变形为(2x-y-1)k-(x-2y+4)=0
∵直线过定点,与k无关
∴
解得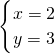 故选B
故选B
方法2:(特殊值法)
无论k取何值,不妨取k= ,得y=3
,得y=3
取k=3,得x=2
而直线x=2与y=3的交点为(2,3)
故选B
点评:本题考查恒过定点的直线以及直线的交点,利用系数为0解决问题;同时考查特殊值法解决填空题,是基础题.
分析:方法1:不论k为何值直线恒过定点,即跟参数k无关,原直线方程可整理为(2x-y-1)k-(x-2y+4)=0,k的系数为0,解方程组即可.
方法2:因为是选择题,跟k无关,不妨取两个特殊值,确定两条直线求交点即可.
解答:方法1:直线方程(2k-1)x-(k-2)y-(k+4)=0
变形为(2x-y-1)k-(x-2y+4)=0
∵直线过定点,与k无关
∴

解得
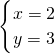 故选B
故选B方法2:(特殊值法)
无论k取何值,不妨取k=
 ,得y=3
,得y=3取k=3,得x=2
而直线x=2与y=3的交点为(2,3)
故选B
点评:本题考查恒过定点的直线以及直线的交点,利用系数为0解决问题;同时考查特殊值法解决填空题,是基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
不论k为何值,直线(2k-1)x-(k-2)y-(k+4)=0恒过的一个定点是( )
| A、(0,0) | B、(2,3) | C、(3,2) | D、(-2,3) |