题目内容
已知函数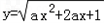 的定义域为R,解关于x的不等式x2﹣x﹣a2+a>0.
的定义域为R,解关于x的不等式x2﹣x﹣a2+a>0.
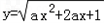 的定义域为R,解关于x的不等式x2﹣x﹣a2+a>0.
的定义域为R,解关于x的不等式x2﹣x﹣a2+a>0.解:因为函数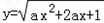 的定义域为R,所以ax2+2ax+1≥0恒成立.(*)
的定义域为R,所以ax2+2ax+1≥0恒成立.(*)
当a=0时,1≥0恒成立,满足题意,
当a≠0时,为满足(*)必有a>0且△=4a2﹣4a≤0,解得0<a≤1,
综上可知:a的取值范围是0≤a≤1.
原不等式可化为(x﹣a)[x﹣(1﹣a)]>0,
当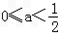 时,不等式的解为:x<a,或x>1﹣a.
时,不等式的解为:x<a,或x>1﹣a.
当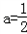 时,不等式的解为:
时,不等式的解为: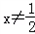 .
.
当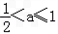 时,不等式的解为:x<1﹣a,或x>a.
时,不等式的解为:x<1﹣a,或x>a.
综上,当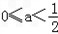 时,不等式的解集为:{x|x<a,或x>1﹣a};
时,不等式的解集为:{x|x<a,或x>1﹣a};
当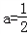 时,不等式的解集为:
时,不等式的解集为: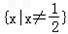 ;
;
当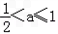 时,不等式的解集为:{x|x<1﹣a或x>a }.
时,不等式的解集为:{x|x<1﹣a或x>a }.
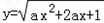 的定义域为R,所以ax2+2ax+1≥0恒成立.(*)
的定义域为R,所以ax2+2ax+1≥0恒成立.(*)当a=0时,1≥0恒成立,满足题意,
当a≠0时,为满足(*)必有a>0且△=4a2﹣4a≤0,解得0<a≤1,
综上可知:a的取值范围是0≤a≤1.
原不等式可化为(x﹣a)[x﹣(1﹣a)]>0,
当
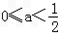 时,不等式的解为:x<a,或x>1﹣a.
时,不等式的解为:x<a,或x>1﹣a.当
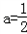 时,不等式的解为:
时,不等式的解为: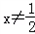 .
.当
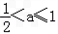 时,不等式的解为:x<1﹣a,或x>a.
时,不等式的解为:x<1﹣a,或x>a.综上,当
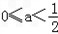 时,不等式的解集为:{x|x<a,或x>1﹣a};
时,不等式的解集为:{x|x<a,或x>1﹣a};当
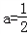 时,不等式的解集为:
时,不等式的解集为: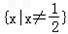 ;
;当
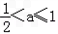 时,不等式的解集为:{x|x<1﹣a或x>a }.
时,不等式的解集为:{x|x<1﹣a或x>a }.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的定义域为R,且当
的定义域为R,且当 时,
时, 恒成立,
恒成立, 对称;
对称; 图象的一个对称点。
图象的一个对称点。 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且
 N*),则
N*),则 的值为( )
的值为( ) 的定义域为R,它的反函数为
的定义域为R,它的反函数为 ,如果
,如果 与
与 互为反函数,且
互为反函数,且 ,则
,则 的值为(
)
的值为(
) B、0
C、
B、0
C、 D、
D、
 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且 (
( N*),则
N*),则 的值为( )
的值为( )