题目内容
给出下面的数表序列:
其中表n(n=1,2,3 …)有n行,第1行的n个数是1,3,5,…2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和.
(I)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明);
(II)每个数列中最后一行都只有一个数,它们构成数列1,4,12…,记此数列为{bn}求和:
| b3 |
| b1b2 |
| b4 |
| b2b3 |
| bn+2 |
| bnbn+1 |
分析:(1)根据表1,表2,表3的规律可写出表4,然后求出各行的平均数,可确定等比数列的首项和公比,进而推广到n.
(2)先求出表n的首项的平均数,进而可确定它的各行中的数的平均数按从上到下的顺序构成首项为n,公比为2的等比数列,进而得到表中最后一行的数bn=n•2n-1,再化简通项
,最后根据裂项法求和.
(2)先求出表n的首项的平均数,进而可确定它的各行中的数的平均数按从上到下的顺序构成首项为n,公比为2的等比数列,进而得到表中最后一行的数bn=n•2n-1,再化简通项
| bk+2 |
| bkbk+1 |
解答:解:(I)表4为
1 3 5 7
4 8 12
12 20
32
它的第1,2,3,4行中的数的平均数分别是4,8,16,32,它们构成首项为4,公比为2的等比数列
将这一结论推广到表n(n≥3),即
表n(n≥3)各行中的数的平均数按从上到下的顺序构成首项为n,公比为2的等比数列.
(II)表n的第1行是1,3,5,…,2n-1,其平均数是
=n
由(I)知,它的各行中的数的平均数按从上到下的顺序构成首项为n,公比为2的等比数列(从而它的第k行中数的平均数是
n•2k-1),于是,表中最后一行的唯一一个数为bn=n•2n-1.
因此
=
=
=
=
-
(k=1,2,…,n)
故
+
+…+
=(
-
)+(
-
)+…+[
-
]
=
-
=4-
.
1 3 5 7
4 8 12
12 20
32
它的第1,2,3,4行中的数的平均数分别是4,8,16,32,它们构成首项为4,公比为2的等比数列
将这一结论推广到表n(n≥3),即
表n(n≥3)各行中的数的平均数按从上到下的顺序构成首项为n,公比为2的等比数列.
(II)表n的第1行是1,3,5,…,2n-1,其平均数是
| 1+3+5+…+(2n-1) |
| n |
由(I)知,它的各行中的数的平均数按从上到下的顺序构成首项为n,公比为2的等比数列(从而它的第k行中数的平均数是
n•2k-1),于是,表中最后一行的唯一一个数为bn=n•2n-1.
因此
| bk+2 |
| bkbk+1 |
| (k+2)2k+1 |
| k•2k-1•(k+1)•2k |
| k+2 |
| k(k+1)•2k-2 |
| 2(k+1)-k |
| k(k+1)•2k-2 |
| 1 |
| k•2k-3 |
| 1 |
| (k+1)•2k-2 |
故
| b3 |
| b1b2 |
| b4 |
| b2b3 |
| bn+2 |
| bnbn+1 |
| 1 |
| 1×2-2 |
| 1 |
| 2×2-1 |
| 1 |
| 2×2-1 |
| 1 |
| 3×20 |
| 1 |
| n×2n-3 |
| 1 |
| (n+1)×2n-2 |
=
| 1 |
| 1×2-2 |
| 1 |
| (n+1)×2n-2 |
| 1 |
| (n+1)×2n-2 |
点评:本题主要考查数列求和和等比数列的性质.数列求和是高考的必考点,一般有公式法、裂项法、错位相减法等,都要熟练掌握.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目

 给出下面的数表序列:其中表n(n=1,2,3…)有n行,第1行的n个数是1,3,5,…2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和.写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明).
给出下面的数表序列:其中表n(n=1,2,3…)有n行,第1行的n个数是1,3,5,…2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和.写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明). 的数表序列:
的数表序列: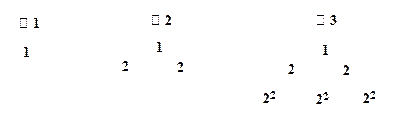
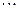 )有n行,表中每一个数“两脚”的两数都是此数的2倍,记表n中所有的数之和为
)有n行,表中每一个数“两脚”的两数都是此数的2倍,记表n中所有的数之和为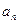 ,例如
,例如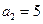 ,
,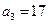 ,
, .则
.则 .
. 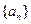 的通项
的通项