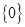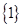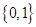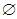题目内容
已知奇函数f(x)列任意的正实数x1,x2(x1≠x2),恒有( ) (x1-x2)( (x1)-f(x2)>0),则一定正确的是
| A.f(4)>f(一6) | B.f(一4)<f(一6) |
| C.f(一4)>f(一6) | D.f(4)<f(一6) |
C
解析试题分析:该题考查抽象函数的运算,显然(4—6)(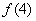 一
一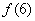 ))>0
))>0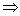
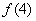 <
<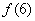 ,结合奇函数的定义,得—
,结合奇函数的定义,得—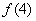 =
=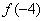 ,一
,一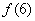 =
=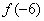 ,故
,故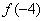 >
>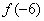 ,故选C
,故选C
考点:函数的奇偶性
点评:解决的关键是利用奇偶性和该函数的单调性来进行大小比较,属于基础题。

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
函数y=xlnx在区间 (0,1)上是 ( )
| A.单调增函数 |
| B.单调减函数 |
C.在(0,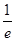 )上是减函数,在( )上是减函数,在(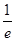 ,1)上是增函数 ,1)上是增函数 |
D.在(0,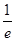 )上是增函数,在( )上是增函数,在(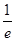 ,1)上是减函数 ,1)上是减函数 |
函数f(x)的定义域为R且满足:f(x)是偶函数,f(x-1)是奇函数,若f(0.5)=9则f(8.5)等于
| A.0 | B.9 | C.-3 | D.-9 |
偶函数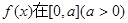 上是单调函数,且
上是单调函数,且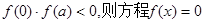 在
在 内根的个数是( ).
内根的个数是( ).
| A.1个 | B.2个 | C.3个 | D.0个 |
直线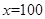 与函数
与函数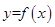 的图象的交点个数是 ( )
的图象的交点个数是 ( )
| A.0 | B.1 | C.0或1 | D.以上均不对 |
下列结论中正确的是
| A.导数为零的点一定是极值点 |
B.如果在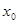 附近的左侧 附近的左侧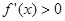 ,右侧 ,右侧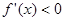 ,那么 ,那么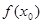 是极大值 是极大值 |
C.如果在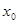 附近的左侧 附近的左侧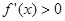 ,右侧 ,右侧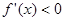 ,那么 ,那么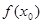 是极小值 是极小值 |
D.如果在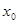 附近的左侧 附近的左侧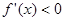 ,右侧 ,右侧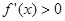 ,那么 ,那么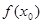 是极大值 是极大值 |
下表表示y是x的函数,则函数的值域是( )
| x | 0<x<5 | 5≤x<10 | 10≤x<15 | 15≤x≤20 |
| y | 2 | 3 | 4 | 5 |
 的图象为折线
的图象为折线 ,设
,设 ,则函数
,则函数 的图象为( )
的图象为( )




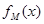 的定义域为R,且定义如下:
的定义域为R,且定义如下: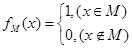 (其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足
(其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足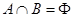 ,则函数
,则函数 的值域为 ( )
的值域为 ( )