题目内容
【题目】已知函数![]() R.
R.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 当a≤0,![]() 在(0,2)上单调递增,在(2,+∞)递减;当
在(0,2)上单调递增,在(2,+∞)递减;当![]() ,
,![]() 在(0,2)和
在(0,2)和![]() 上单调递增,在(2,
上单调递增,在(2,![]() )递减;当a=
)递减;当a=![]() ,
,![]() 在(0,+∞)递增;当a>
在(0,+∞)递增;当a>![]() ,
,![]() 在(0,
在(0,![]() )和(2,+∞)上单调递增,在(
)和(2,+∞)上单调递增,在(![]() ,2)递减;(2)
,2)递减;(2) ![]() .
.
【解析】
(1)求出![]() ,分四种情况讨论
,分四种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)由(1)知当
的减区间;(2)由(1)知当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,又
,又![]() ,取
,取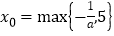 ,可证明
,可证明![]() ,
,![]() 有两个零点等价于
有两个零点等价于![]() ,得
,得![]() ,可证明,当
,可证明,当![]() 时与当
时与当![]() 且
且![]() 时,至多一个零点,综合讨论结果可得结论.
时,至多一个零点,综合讨论结果可得结论.
(1)![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
(i)当![]() 时,
时,![]() 恒成立,
恒成立,
![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
![]() 时,
时,![]() 在
在![]() 上单调递减.
上单调递减.
(ii)当![]() 时,由
时,由![]() 得,
得,![]() (舍去),
(舍去),
①当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() ,即
,即![]() 时,
时,![]() 或
或![]() ,
,
![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增;
上单调递增;
![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递减.
上单调递减.
③当![]() ,即
,即![]() 时,
时,![]() 或
或![]() 时,
时,![]() 恒成立,
恒成立,
![]() 在
在![]() 单调递增,
单调递增,
![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,无单调递减区间为;
,无单调递减区间为;
当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由(1)知当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
又![]() ,取
,取![]() ,令
,令![]() ,
,
则![]() 在
在![]() 成立,故
成立,故![]() 单调递增,
单调递增,
![]() ,
,
![]() ,
,
![]() 有两个零点等价于
有两个零点等价于![]() ,得
,得![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,只有一个零点,不符合题意;
,只有一个零点,不符合题意;
当![]() 时,
时,![]() 在
在![]() 单调递增,至多只有一个零点,不符合题意;
单调递增,至多只有一个零点,不符合题意;
当![]() 且
且![]() 时,
时,![]() 有两个极值,
有两个极值,
![]() ,
,
记![]() ,
,
![]() ,
,
令![]() ,则
,则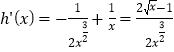 ,
,
当![]() 时,
时,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 在
在![]() 单调递减,
单调递减,
故![]() 在
在![]() 单调递增,
单调递增,
![]() 时,
时,![]() ,故
,故![]() ,
,
又![]() ,
,
由(1)知,![]() 至多只有一个零点,不符合题意,
至多只有一个零点,不符合题意,
综上,实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】将标号为1,2,…,20的20张卡片放入下列表格中,一个格放入一张卡片,选出每列标号最小的卡片,将这些卡片中标号最大的数设为![]() ;选出每行标号最大的卡片,将这些卡片中标号最小的数设为
;选出每行标号最大的卡片,将这些卡片中标号最小的数设为![]() .
.
甲同学认为![]() 有可能比
有可能比![]() 大,乙同学认为
大,乙同学认为![]() 和
和![]() 有可能相等,那么甲乙两位同学的说法中( )
有可能相等,那么甲乙两位同学的说法中( )
A. 甲对乙不对 B. 乙对甲不对 C. 甲乙都对 D. 甲乙都不对
