题目内容
若点P（a，3）到直线4x-3y+1=0的距离为4，且该点在不等式2x+y＜3所表示的平面区域内，则a的值为（ ）
| A、7 | B、-7 | C、3 | D、-3 |
分析：根据点到直线的距离公式表示出P点到直线4x-3y+1=0的距离，让其等于4列出关于a的方程，求出a的值，然后又因为P在不等式2x+y＜3所表示的平面区域内，如图阴影部分表示不等式2x+y＜3所表示的平面区域，可判断出满足题意的a的值．
解答：解：点P到直线4x-3y+1=0的距离d=
=4，则4a-8=20或4a-8=-20，解得a=7或-3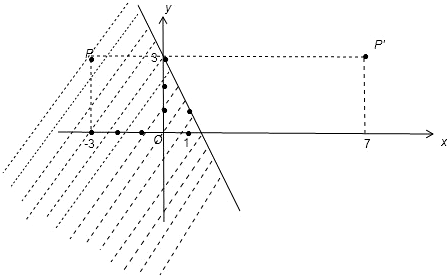
因为P点在不等式2x+y＜3所表示的平面区域内，根据图象可知a=7不满足题意，舍去．所以a的值为-3
故选D
| |4a-9+1| | ||
|
因为P点在不等式2x+y＜3所表示的平面区域内，根据图象可知a=7不满足题意，舍去．所以a的值为-3
故选D
点评：考查学生灵活运用点到直线的距离公式化简求值，理解二元一次不等式表示的平面区域，会利用数形结合的数学思想解决实际问题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
过点A（a,0）,B(0,b)的直
，原点到该直线的距离为
.
求直线MN的方程；
交椭圆于P、Q两点，以PQ为直径的圆过点D（1，0）？若存在，求出k的值；若不存在，请说明理由。