题目内容
【题目】已知函数![]() .
.
(1)求![]() 的最小正周期
的最小正周期![]() ;
;
(2)设![]() ,若
,若![]() 在
在![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的值;
的值;
(3)若![]() 对任意的
对任意的![]() 和
和![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】试题分析:(1)化简![]()
![]() 最小正周期
最小正周期![]() ;(2)当
;(2)当![]() 时,
时, ![]() .令
.令![]() ,则
,则![]() .
.
原函数可化为![]() ,
, ![]() .再利用分类讨论思想,对
.再利用分类讨论思想,对![]() 求得
求得![]() 或
或![]() ;(3)由(2)可知,当
;(3)由(2)可知,当![]() 时,
时, ![]() .①当
.①当![]() 为偶数时,
为偶数时, ![]()
![]()
![]() .
. ![]()
![]() .②当
.②当![]() 为奇数时,
为奇数时, ![]() 的取值范围是
的取值范围是![]() .
.
试题解析:(1)![]()
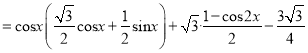
![]()
![]()
![]()
![]() .
.
![]() 的最小正周期
的最小正周期![]() .
.
(2)由(1)知![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,
,
即![]() .
.
令![]() ,则
,则![]() .
.
![]() ,
, ![]() .
.
令![]() ,
, ![]() .易知
.易知![]() .
.
①当![]() 时,
时, ![]() 在
在![]() 上为增函数,
上为增函数,
因此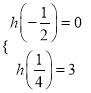 ,即
,即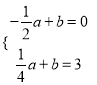 .解得
.解得![]() .
.
②当![]() 时,
时, ![]() 在
在![]() 上为减函数,
上为减函数,
因此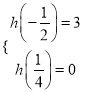 ,即
,即 .解得
.解得![]() .
.
综上所述, ![]() 或
或![]() .
.
(3)由(2)可知,当![]() 时,
时, ![]() .
.
①当![]() 为偶数时,
为偶数时, ![]()
![]()
![]() .
.
由题意,只需![]() .
.
因为当![]() 时,
时, ![]() ,所以
,所以![]() .
.
②当![]() 为奇数时,
为奇数时, ![]()
![]()
![]() .
.
由题意,只需![]() .
.
因为当![]() 时,
时, ![]() ,所以
,所以![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目