Question

1．函数y=|x+1|的单调递增区间为[-1，+∞），单调递减区间为（-∞，-1]．

Answer 1

分析 利用零点分段法，将函数化为分段函数，进而画出函数的图象，数形结合，可得答案．

解答 解：函数y=|x+1|=$\left\{\begin{array}{l}-x-1，x＜-1\\ x+1，x≥-1\end{array}\right.$的图象如下图所示：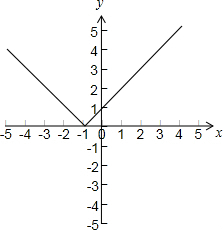

由图可得：函数y=|x+1|的单调递增区间为[-1，+∞），
函数y=|x+1|的单调递减区间为（-∞，-1]，
故答案为：[-1，+∞），（-∞，-1]

点评 本题考查的知识点是分段函数的应用，难度不大，属于基础题．