题目内容
已知椭圆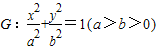 的离心率为
的离心率为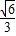 ,右焦点为 (
,右焦点为 (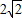 ,0).斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
,0).斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2).(Ⅰ)求椭圆G的方程;
(Ⅱ)求△PAB的面积.
【答案】分析:(Ⅰ)由椭圆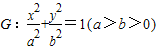 的离心率为
的离心率为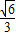 ,右焦点为 (
,右焦点为 (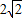 ,0),知
,0),知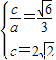 ,由此能求出椭圆G的方程.
,由此能求出椭圆G的方程.
(Ⅱ)设l:y=x+b,代入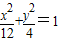 ,得4x2+6bx+3b2-12=0,根据韦达定理
,得4x2+6bx+3b2-12=0,根据韦达定理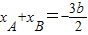 ,
,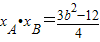 ,故yA+yB=
,故yA+yB=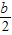 ,由此能求出△PAB的面积.
,由此能求出△PAB的面积.
解答:解:(Ⅰ)∵椭圆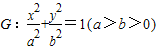 的离心率为
的离心率为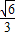 ,右焦点为 (
,右焦点为 (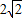 ,0),
,0),
∴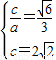 ,解得a=2
,解得a=2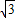 ,
,
∴b=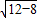 =2,
=2,
∴椭圆G的方程为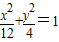 .
.
(Ⅱ)设l:y=x+b,
代入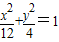 ,得4x2+6bx+3b2-12=0,
,得4x2+6bx+3b2-12=0,
根据韦达定理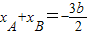 ,
,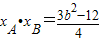 ,
,
∴yA+yB=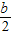 ,
,
设M为AB的中点,则M(-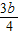 ,
,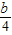 ),AB的中垂线的斜率k=-1,
),AB的中垂线的斜率k=-1,
∴AB的中垂线:x+y+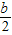 =0,将P(-3,2)代入,得b=2,
=0,将P(-3,2)代入,得b=2,
∴l:x-y+2=0,根据弦长公式可得AB=3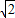 ,d=
,d=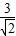 ,
,
∴S△PAB=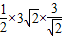 =
= .
.
点评:本题考查椭圆方程和三角形面积的求法,具体涉及到椭圆的简单性质、直线和椭圆的位置关系、根与系数的关系、根的判别式、中垂线方程的求法、弦长公式等基本知识点,解题时要认真审题,注意等价转化思想的灵活运用.
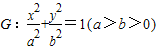 的离心率为
的离心率为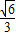 ,右焦点为 (
,右焦点为 (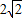 ,0),知
,0),知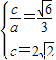 ,由此能求出椭圆G的方程.
,由此能求出椭圆G的方程.(Ⅱ)设l:y=x+b,代入
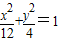 ,得4x2+6bx+3b2-12=0,根据韦达定理
,得4x2+6bx+3b2-12=0,根据韦达定理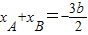 ,
,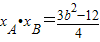 ,故yA+yB=
,故yA+yB=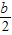 ,由此能求出△PAB的面积.
,由此能求出△PAB的面积.解答:解:(Ⅰ)∵椭圆
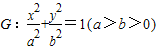 的离心率为
的离心率为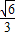 ,右焦点为 (
,右焦点为 (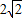 ,0),
,0),∴
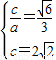 ,解得a=2
,解得a=2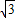 ,
,∴b=
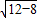 =2,
=2,∴椭圆G的方程为
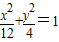 .
.(Ⅱ)设l:y=x+b,
代入
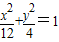 ,得4x2+6bx+3b2-12=0,
,得4x2+6bx+3b2-12=0,根据韦达定理
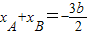 ,
,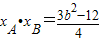 ,
,∴yA+yB=
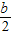 ,
,设M为AB的中点,则M(-
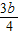 ,
,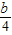 ),AB的中垂线的斜率k=-1,
),AB的中垂线的斜率k=-1,∴AB的中垂线:x+y+
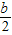 =0,将P(-3,2)代入,得b=2,
=0,将P(-3,2)代入,得b=2,∴l:x-y+2=0,根据弦长公式可得AB=3
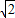 ,d=
,d=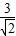 ,
,∴S△PAB=
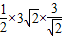 =
= .
.点评:本题考查椭圆方程和三角形面积的求法,具体涉及到椭圆的简单性质、直线和椭圆的位置关系、根与系数的关系、根的判别式、中垂线方程的求法、弦长公式等基本知识点,解题时要认真审题,注意等价转化思想的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: