题目内容
已知正项数列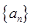 满足:
满足: ,设
,设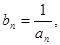 数列
数列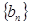 的前
的前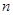 项的和
项的和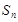 ,则
,则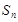 的取值范围为( )
的取值范围为( )
A.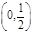 B.
B.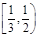 C.
C. D.
D.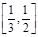
【答案】
B
【解析】
试题分析:因为,(2n-1)an+2=(2n+1)an-1+8n2(n>1,n∈N*),
所以,(2n-1)an-(2n+1)an-1=2(4n2-1),
又n>1,等式两端同除以4n2-1得: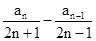 =2,即数列{
=2,即数列{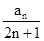 }是以1为首项,2为公差的等差数列.
}是以1为首项,2为公差的等差数列.
所以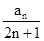 =1+(n-1)×2=2n-1,
=1+(n-1)×2=2n-1,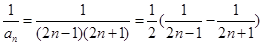 ,
,
∴sn=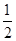 [(1-
[(1-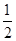 )+(
)+(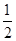 -
-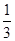 )+(
)+(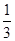 -
-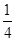 )+……+
)+……+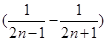 ]=
]=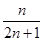 .
.
当n=1时,s1=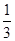 ;n→+∞时,sn→
;n→+∞时,sn→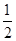 ,
,
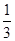 ≤ sn<
≤ sn<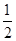 ,故答案为B.
,故答案为B.
考点:本题主要考查数列的概念,等差数列的基础知识,“裂项相消法”,“放缩法”证明不等式。
点评:中档题,本题综合考查等差数列、等比数列的基础知识,本解答从确定通项公式入手,明确了所研究数列的特征。“分组求和法”、“错位相消法”、“裂项相消法”是高考常常考到数列求和方法。先求和,再根据和的特征证明不等式,是常用方法。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 满足:
满足: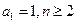 时,
时,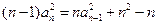 。
。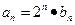 ,数列
,数列 的前n项和为
的前n项和为 ,是否存在正整数m,使得对任意的
,是否存在正整数m,使得对任意的
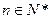 ,
,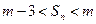 恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
恒成立?若存在,求出所有的正整数m;若不存在,说明理由。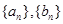 满足:对任意正整数
满足:对任意正整数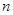 ,都有
,都有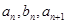 成等差数列,
成等差数列,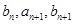 成等比数列,且
成等比数列,且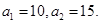
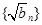 是等差数列;
是等差数列;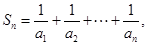 如果对任意正整数
如果对任意正整数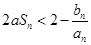 恒成立,求实数
恒成立,求实数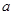 的取值范围.
的取值范围.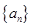 满足:
满足: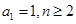 时,
时,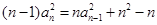 。
。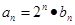 ,数列
,数列 的前n项和为
的前n项和为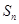 ,是否存在正整数m,使得对任意的
,是否存在正整数m,使得对任意的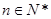 ,
,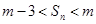 恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
恒成立?若存在,求出所有的正整数m;若不存在,说明理由。