题目内容
已知正项数列 满足:
满足: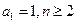 时,
时,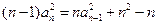 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设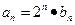 ,数列
,数列 的前n项和为
的前n项和为 ,是否存在正整数m,使得对任意的
,是否存在正整数m,使得对任意的
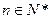 ,
,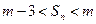 恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
解:①由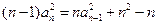
得
令 ∴
∴ (
( )
) 而
而
∴ 即
即
即 ,由正项数列知
,由正项数列知 ………………6分
………………6分
②由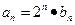 得
得

∴ 的
的 而
而 的
的
∴当m=2或m=3时
使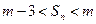 恒成立……
恒成立…… …………13分
…………13分
解析

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
题目内容
已知正项数列 满足:
满足: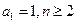 时,
时,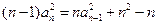 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设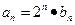 ,数列
,数列 的前n项和为
的前n项和为 ,是否存在正整数m,使得对任意的
,是否存在正整数m,使得对任意的
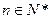 ,
,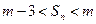 恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
解:①由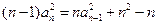
得
令 ∴
∴ (
( )
) 而
而
∴ 即
即
即 ,由正项数列知
,由正项数列知 ………………6分
………………6分
②由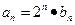 得
得

∴ 的
的 而
而 的
的
∴当m=2或m=3时
使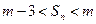 恒成立……
恒成立…… …………13分
…………13分
解析

 全能测控期末小状元系列答案
全能测控期末小状元系列答案