题目内容
（本题12分）已知
，
⑴若
，求方程
的解；
⑵若关于
的方程在
上有两个解
，求
的取值范围，
并证明：
解：（1）当k＝2时， 
----1分
① 当
，即
或
时，方程化为
解得
，因为
，舍去，
所以
． ----3分
②当
，即
时，方程化为
解得
-----4分
由①②得当k＝2时，方程
的解为或．---5分
⑵不妨设0＜
＜
＜2，
因为
所以
在（0,1］是单调函数，故
在（0,1］上至多一个解，
若1＜＜＜2，则
＜0，故不符题意，因此0＜≤1＜＜2．--7分
由
得
， 所以
；
由
得
， 所以
； -----9分
故当时，方程在(0，2)上有两个解． -----10分
因为0＜≤1＜＜2，所以，
消去k 得 
-----11分
即
因为x2＜2，所以
． -----14分
练习册系列答案
相关题目
的图像关于原点对称，并且当
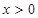时，
，试求
上的表达式，并画出它的图像，根据图像写出它的单调区间。
（1）求
的定义域；（2）求
关于点
对称.
的值.
．
时，求函数
的单调递减区间；
时，
上恒大于0，求实数
的取值范围．
的不等式
，其中
.
变化时，试求不等式的解集
； 
（其中
为整数集）. 试探究集合
能否为有限集？若能，求出使得集合