题目内容
设（3-x）5=a+a1（x-1）+a2（x-1）2+…+a5（x-1）5，那么a+a2+a4的值为（ ）A．123
B．122
C．246
D．244
【答案】分析：利用展开式，分别令x=2与0，两式相加可得结论．
解答：解：x=2时，（3-2）5=a+a1+a2+a3+a4+a5；x=0时，（3-0）5=a-a1+a2-a3+a4-a5，
∴a+a2+a4=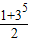
=122
故选B．
点评：本题考查二项式的系数问题，考查赋值法的运用，属于基础题．
解答：解：x=2时，（3-2）5=a+a1+a2+a3+a4+a5；x=0时，（3-0）5=a-a1+a2-a3+a4-a5，
∴a+a2+a4=
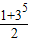=122故选B．
点评：本题考查二项式的系数问题，考查赋值法的运用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目