题目内容
已知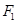 、
、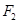 分别是椭圆
分别是椭圆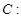
 的左、右焦点,右焦点
的左、右焦点,右焦点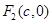 到上顶点的距离为2,若
到上顶点的距离为2,若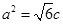
(Ⅰ)求此椭圆 的方程;
的方程;
(Ⅱ)直线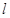 与椭圆
与椭圆 交于
交于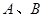 两点,若弦
两点,若弦 的中点为
的中点为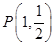 ,求直线
,求直线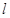 的方程.
的方程.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)求此椭圆 的方程,由题意
的方程,由题意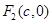 到上顶点的距离为2,即
到上顶点的距离为2,即 ,
,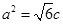 ,再由
,再由 ,即可求出
,即可求出 ,从而得椭圆的方程;(Ⅱ)直线
,从而得椭圆的方程;(Ⅱ)直线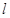 与椭圆
与椭圆 交于
交于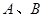 两点,若弦
两点,若弦 的中点为
的中点为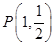 ,求直线
,求直线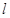 的方程,可采用设而不求的方法,即设
的方程,可采用设而不求的方法,即设 ,将
,将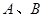 代入椭圆方程,两式作差即可得直线
代入椭圆方程,两式作差即可得直线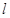 的斜率,再由点斜式写出直线方程.
的斜率,再由点斜式写出直线方程.
试题解析:(Ⅰ)由题意得
 所以
所以
(Ⅱ)设 ,
, ,
,

 AB:
AB: ,即
,即
考点:椭圆方程,直线与椭圆位置关系.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
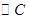 :
: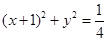 ,
,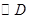 :
: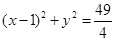 .动点P与
.动点P与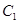 的方程;
的方程;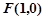 ,点
,点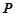 是点
是点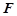 关于
关于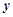 轴的对称点,过点
轴的对称点,过点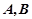 两点。
两点。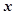 轴上是否存在不同于点
轴上是否存在不同于点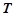 ,使得
,使得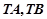 与
与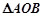 的面积为
的面积为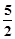 ,求向量
,求向量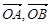 的夹角;
的夹角;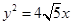 的焦点重合.
的焦点重合. 交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得
交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得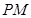 始终平分
始终平分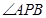 ?若存在求出
?若存在求出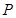 点坐标;若不存在请说明理由.
点坐标;若不存在请说明理由.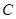 :
: ,
,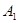 、
、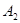 、
、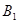 、
、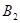 为椭圆
为椭圆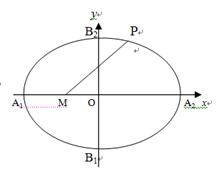
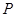 到焦点距离的最大值为
到焦点距离的最大值为 ,最小值为
,最小值为 ,求椭圆方程;
,求椭圆方程;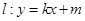 相交于
相交于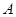 ,
,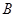 两点(
两点(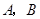 不是椭圆的左右顶点),并满足
不是椭圆的左右顶点),并满足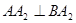 试研究:直线
试研究:直线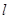 是否过定点? 若过定点,请求出定点坐标,若不过定点,请说明理由
是否过定点? 若过定点,请求出定点坐标,若不过定点,请说明理由 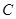 的中心为直角坐标系
的中心为直角坐标系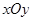 的原点,焦点在
的原点,焦点在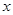 轴上,它的一个顶点到两个焦点的距离分别是7和1.
轴上,它的一个顶点到两个焦点的距离分别是7和1.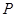 为椭圆
为椭圆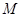 为过
为过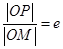 (
(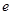 为椭圆的离心率),求点
为椭圆的离心率),求点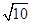 时,求k的值.
时,求k的值. 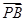 |,
|, |
|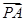 |,8成等差数列.
|,8成等差数列.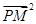 ,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?