题目内容
（13分）设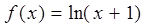
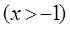
(1)讨论函数
的单调性。
（2）求证：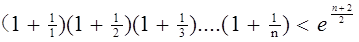
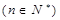
（1）
；（2）原命题等价于证明
。
解析试题分析：（1）
令
两根为
（2）原命题等价于证明
方法一用数学归纳法证明
方法二由（1）知
令
得
只需证
即可，即
考点：利用导数研究函数的 单调性；数学归纳法；放缩法；一元二次不等式的解法。
点评：利用导数求函数的单调区间，一定要先求函数的定义域，不然容易出错。
练习册系列答案
相关题目
题目内容
（13分）设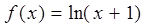
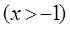
(1)讨论函数 的单调性。
（2）求证：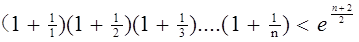
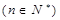
（1）；（2）原命题等价于证明。
解析试题分析：（1）令 两根为
（2）原命题等价于证明
方法一用数学归纳法证明
方法二由（1）知
令得
只需证即可，即
考点：利用导数研究函数的 单调性；数学归纳法；放缩法；一元二次不等式的解法。
点评：利用导数求函数的单调区间，一定要先求函数的定义域，不然容易出错。
；
，求
在[－2，2] 上的最大值和最小值；
，
的单调区间和极值点；
，记过点
与原点的直线斜率为
。是否存在
使
？若存在，求出
。
如果
，函数在区间
上存在极值，求实数a的取值范围；
当
时，不等式
恒成立，求实数k的取值范围。
=
（
为自然对数的底数），
，记
．
为
的导函数，判断函数
的单调性，并加以证明；
=0有两个零点，求实数
的取值范围．
，（
为自然对数的底数）。
时，求函数
在区间
上的最大值和最小值； 
，在
上总存在两个不同的
，使得
成立，求
的取值范围。
.
在点
处的切线与直线
垂直，求函数
都有
成立，试求
的取值范围；
.当
时，函数
在区间
上有两个零点，求实数
的取值范围.
,其中
，曲线
在点
处的切线方程为
。
，
的值；
，且
时，
，求
的取值范围。