题目内容
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC= ![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD. 
(Ⅰ)证明:ED∥面PAB;
(Ⅱ)若PC=2,PA= ![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
【答案】(Ⅰ)证明:取PB的中点F,连接AF,EF. ∵EF是△PBC的中位线,∴EF∥BC,且EF= ![]() .
.
又AD=BC,且AD= ![]() ,∴AD∥EF且AD=EF,
,∴AD∥EF且AD=EF,
则四边形ADEF是平行四边形.
∴DE∥AF,又DE面ABP,AF面ABP,
∴ED∥面PAB;
(Ⅱ)解:法一、取BC的中点M,连接AM,则AD∥MC且AD=MC,
∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上.
∴AB⊥AC,可得 ![]() .
.
过D作DG⊥AC于G,
∵平面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,
∴DG⊥平面PAC,则DG⊥PC.
过G作GH⊥PC于H,则PC⊥面GHD,连接DH,则PC⊥DH,
∴∠GHD是二面角A﹣PC﹣D的平面角.
在△ADC中, ![]() ,连接AE,
,连接AE, ![]() .
.
在Rt△GDH中, ![]() ,
,
∴ ![]() ,
,
即二面角A﹣PC﹣D的余弦值 ![]() .
.
法二、取BC的中点M,连接AM,则AD∥MC,且AD=MC.
∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上,
∴AB⊥AC.
∵面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,∴AB⊥面PAC.
如图以A为原点, ![]() 方向分别为x轴正方向,y轴正方向建立空间直角坐标系.
方向分别为x轴正方向,y轴正方向建立空间直角坐标系.
可得 ![]() ,
, 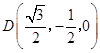 .
.
设P(x,0,z),(z>0),依题意有 ![]() ,
, ![]() ,
,
解得 ![]() .
.
则  ,
,  ,
,  .
.
设面PDC的一个法向量为 ![]() ,
,
由 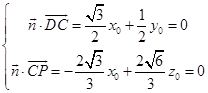 ,取x0=1,得
,取x0=1,得  .
.![]() 为面PAC的一个法向量,且
为面PAC的一个法向量,且 ![]() ,
,
设二面角A﹣PC﹣D的大小为θ,
则有  ,即二面角A﹣PCD的余弦值
,即二面角A﹣PCD的余弦值 ![]() .
.

【解析】(Ⅰ)取PB的中点F,连接AF,EF,由三角形的中位线定理可得四边形ADEF是平行四边形.得到DE∥AF,再由线面平行的判定可得ED∥面PAB;(Ⅱ)法一、取BC的中点M,连接AM,由题意证得A在以BC为直径的圆上,可得AB⊥AC,找出二面角A﹣PC﹣D的平面角.求解三角形可得二面角A﹣PC﹣D的余弦值. 法二、由题意证得AB⊥AC.又面PAC⊥平面ABCD,可得AB⊥面PAC.以A为原点, ![]() 方向分别为x轴正方向,y轴正方向建立空间直角坐标系.求出P的坐标,再求出平面PDC的一个法向量,由图可得
方向分别为x轴正方向,y轴正方向建立空间直角坐标系.求出P的坐标,再求出平面PDC的一个法向量,由图可得 ![]() 为面PAC的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PC﹣D的余弦值.
为面PAC的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PC﹣D的余弦值.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案