题目内容
在数列{
}中,a1=2,an+1=an+2n(n∈N*),
(1)求{
}的通项公式;
(2)求数列{nan}的前n项和Sn.
| a | n |
(1)求{
| a | n |
(2)求数列{nan}的前n项和Sn.
分析:(1)利用递推公式,结合累加法,可求{
}的通项公式;
(2)利用错位相减法,可求数列{nan}的前n项和Sn.
| a | n |
(2)利用错位相减法,可求数列{nan}的前n项和Sn.
解答:解:(1)∵an+1=an+2n(n∈N*),
∴an+1-an=2n,
∵a1=2,
∴an=a1+(a2-a1)+…+(an-an-1)=2+2+4+…+2n-1=2n;
(2)∵nan=n•2n,
∴Sn=1•2+2•22+…+n•2n,①
∴2Sn=1•22+2•23+…+n•2n+1,②
①-②:-Sn=1•2+1•22+1•23+…+1•2n-n•2n+1=2•
-n•2n+1=2(2n-1)-n•2n+1,
∴Sn=-2(2n-1)+n•2n+1.
∴an+1-an=2n,
∵a1=2,
∴an=a1+(a2-a1)+…+(an-an-1)=2+2+4+…+2n-1=2n;
(2)∵nan=n•2n,
∴Sn=1•2+2•22+…+n•2n,①
∴2Sn=1•22+2•23+…+n•2n+1,②
①-②:-Sn=1•2+1•22+1•23+…+1•2n-n•2n+1=2•
| 1-2n |
| 1-2 |
∴Sn=-2(2n-1)+n•2n+1.
点评:本题考查了利用递推公式求数列的通项公式,考查了累加法,考查错位相减法,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
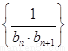 的前n项和Tn.
的前n项和Tn.