Question

已知复数z=（x-2）+yi（x，y∈R）的模为

3

，则

y

x

的取值范围是

 

．

Answer 1

分析：根据复数的模，利用模长公式得：（x-2）²+y²=3，根据

y

x

表示动点（x，y）与原点（0，0）连线的斜率．根据直线与圆相切的性质得到结果

解答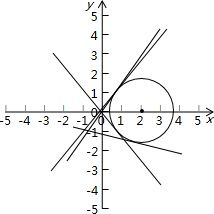：解：∵复数（x-2）+yi（x，y∈R）的模为

3

∴（x-2）²+y²=3
根据

y

x

表示动点（x，y）到定点（0，0）的斜率知：

y

x

的最大值是

3

同理求得最小值是-

3

，
∴

y

x

的取值范围是[-

3

，

3

]
故答案为：[-

3

，

3

]

点评：本题考查复数求模及简单线性规划，解答关键是根据复数的模长公式，得到x，y所满足的条件，根据条件做出图形利用数形结合的方法求解．