题目内容
对于函数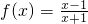 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),令集合
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),令集合 ,则集合M为
,则集合M为
- A.空集
- B.单元素集
- C.二元素集
- D.无限集
C
分析:由函数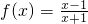 ,f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),能够推导出f2(x)=-
,f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),能够推导出f2(x)=- ,f3(x)=
,f3(x)= ,f4(x)=x,f5(x)=
,f4(x)=x,f5(x)= .故f2012(x)=x,由此能求出集合M.
.故f2012(x)=x,由此能求出集合M.
解答:∵函数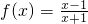 ,f2(x)=f[f(x)],
,f2(x)=f[f(x)],
f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),
∴f2(x)= =-
=- ,
,
f3(x)= =
= ,
,
f4(x)= =x,
=x,
f5(x)= .
.
∵2012=4×503,
∴f2012(x)=x,
∴ ={x|x=
={x|x= }={-1,1}.
}={-1,1}.
故选C.
点评:本题考查函数值的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
分析:由函数
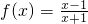 ,f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),能够推导出f2(x)=-
,f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),能够推导出f2(x)=- ,f3(x)=
,f3(x)= ,f4(x)=x,f5(x)=
,f4(x)=x,f5(x)= .故f2012(x)=x,由此能求出集合M.
.故f2012(x)=x,由此能求出集合M.解答:∵函数
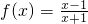 ,f2(x)=f[f(x)],
,f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),
∴f2(x)=
 =-
=- ,
,f3(x)=
 =
= ,
,f4(x)=
 =x,
=x,f5(x)=
 .
.∵2012=4×503,
∴f2012(x)=x,
∴
 ={x|x=
={x|x= }={-1,1}.
}={-1,1}.故选C.
点评:本题考查函数值的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
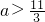 ;
; ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),令集合
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),令集合 ,则集合M为( )
,则集合M为( ) ;
;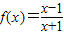 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集. ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),令集合
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…fn+1(x)=f[fn(x)],(n∈N*,且n≥2),令集合 ,则集合M为( )
,则集合M为( )