ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈΣΝΥΦύΩΊΡ≥÷÷ΝψΦΰΒΡ“ΜΧθ…ζ≤ζœΏΒΡ…ζ≤ζΙΐ≥ΧΘ§Φλ―ι‘±ΟΩΧλ¥”ΗΟ…ζ≤ζœΏ…œΥφΜζ≥ι»Γ16ΗωΝψΦΰΘ§≤Δ≤βΝΩΤδ≥Ώ¥γΘ®ΒΞΈΜΘΚ ![]() Θ©Θ°ΗυΨί≥ΛΤΎ…ζ≤ζΨ≠―ιΘ§Ω…“‘»œΈΣ’βΧθ…ζ≤ζœΏ’ΐ≥ΘΉ¥Χ§œ¬…ζ≤ζΒΡΝψΦΰΒΡ≥Ώ¥γΖΰ¥”’ΐΧ§Ζ÷≤Φ
Θ©Θ°ΗυΨί≥ΛΤΎ…ζ≤ζΨ≠―ιΘ§Ω…“‘»œΈΣ’βΧθ…ζ≤ζœΏ’ΐ≥ΘΉ¥Χ§œ¬…ζ≤ζΒΡΝψΦΰΒΡ≥Ώ¥γΖΰ¥”’ΐΧ§Ζ÷≤Φ![]() Θ°
Θ°
Θ®1Θ©ΦΌ…η…ζ≤ζΉ¥Χ§’ΐ≥ΘΘ§Φ«![]() ±μ Ψ“ΜΧλΡΎ≥ι»ΓΒΡ16ΗωΝψΦΰ÷–Τδ≥Ώ¥γ‘Ύ
±μ Ψ“ΜΧλΡΎ≥ι»ΓΒΡ16ΗωΝψΦΰ÷–Τδ≥Ώ¥γ‘Ύ![]() ÷°ΆβΒΡΝψΦΰ ΐΘ§«σ
÷°ΆβΒΡΝψΦΰ ΐΘ§«σ![]() ΦΑ
ΦΑ![]() ΒΡ ΐ―ßΤΎΆϊΘΜ
ΒΡ ΐ―ßΤΎΆϊΘΜ
Θ®2Θ©“ΜΧλΡΎ≥ιΦλΝψΦΰ÷–Θ§»γΙϊ≥ωœ÷ΝΥ≥Ώ¥γ‘Ύ![]() ÷°ΆβΒΡΝψΦΰΘ§ΨΆ»œΈΣ’βΧθ…ζ≤ζœΏ‘Ύ’β“ΜΧλΒΡ…ζ≤ζΙΐ≥ΧΩ…Ρή≥ωœ÷ΝΥ“λ≥Θ«ιΩωΘ§–ηΕ‘Β±ΧλΒΡ…ζ≤ζΙΐ≥ΧΫχ––Φλ≤ιΘ°
÷°ΆβΒΡΝψΦΰΘ§ΨΆ»œΈΣ’βΧθ…ζ≤ζœΏ‘Ύ’β“ΜΧλΒΡ…ζ≤ζΙΐ≥ΧΩ…Ρή≥ωœ÷ΝΥ“λ≥Θ«ιΩωΘ§–ηΕ‘Β±ΧλΒΡ…ζ≤ζΙΐ≥ΧΫχ––Φλ≤ιΘ°
Θ®ΔΓΘ© ‘ΥΒΟς…œ ωΦύΩΊ…ζ≤ζΙΐ≥ΧΖΫΖ®ΒΡΚœάμ–‘ΘΜ
Θ®ΔΔΘ©œ¬Οφ «Φλ―ι‘±‘Ύ“ΜΧλΡΎ≥ι»ΓΒΡ16ΗωΝψΦΰΒΡ≥Ώ¥γΘΚ
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
Ψ≠ΦΤΥψΒΟ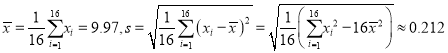 Θ§Τδ÷–
Θ§Τδ÷–![]() ΈΣ
ΈΣ
≥ι»ΓΒΡΒΎ![]() ΗωΝψΦΰΒΡ≥Ώ¥γΘ§
ΗωΝψΦΰΒΡ≥Ώ¥γΘ§ ![]() Θ°
Θ°
”Ο―υ±ΨΤΫΨυ ΐ![]() ΉςΈΣ
ΉςΈΣ![]() ΒΡΙάΦΤ÷Β
ΒΡΙάΦΤ÷Β![]() Θ§”Ο―υ±Ψ±ξΉΦ≤ν
Θ§”Ο―υ±Ψ±ξΉΦ≤ν![]() ΉςΈΣ
ΉςΈΣ![]() ΒΡΙάΦΤ÷Β
ΒΡΙάΦΤ÷Β![]() Θ§άϊ”ΟΙάΦΤ÷Β≈–Εœ «Ζώ–ηΕ‘Β±ΧλΒΡ…ζ≤ζΙΐ≥ΧΫχ––Φλ≤ιΘΩΧό≥ΐ
Θ§άϊ”ΟΙάΦΤ÷Β≈–Εœ «Ζώ–ηΕ‘Β±ΧλΒΡ…ζ≤ζΙΐ≥ΧΫχ––Φλ≤ιΘΩΧό≥ΐ![]() ÷°ΆβΒΡ ΐΨίΘ§”Ο Θœ¬ΒΡ ΐΨίΙάΦΤ
÷°ΆβΒΡ ΐΨίΘ§”Ο Θœ¬ΒΡ ΐΨίΙάΦΤ![]() ΚΆ
ΚΆ![]() Θ®ΨΪ»ΖΒΫ0.01Θ©Θ°
Θ®ΨΪ»ΖΒΫ0.01Θ©Θ°
ΗΫΘΚ»τΥφΜζ±δΝΩ![]() Ζΰ¥”’ΐΧ§Ζ÷≤Φ
Ζΰ¥”’ΐΧ§Ζ÷≤Φ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§ ![]() Θ°
Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§ ![]() ΘΜΘ®2Θ©Θ®iΘ©ΦϊΫβΈωΘ§(ii)
ΘΜΘ®2Θ©Θ®iΘ©ΦϊΫβΈωΘ§(ii) ![]() ,
,![]() .
.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΧβ…ηΧθΦΰ÷Σ“ΜΗωΝψΦΰΒΡ≥Ώ¥γ‘Ύ![]() ÷°ΡΎΒΡΗ≈¬ ΈΣ0.9974Θ§‘ρΝψΦΰΒΡ≥Ώ¥γ‘Ύ
÷°ΡΎΒΡΗ≈¬ ΈΣ0.9974Θ§‘ρΝψΦΰΒΡ≥Ώ¥γ‘Ύ![]() ÷°ΆβΒΡΗ≈¬ ΈΣ0.0026Θ§Εχ
÷°ΆβΒΡΗ≈¬ ΈΣ0.0026Θ§Εχ![]() Θ§ΫχΕχΩ…“‘«σ≥ω
Θ§ΫχΕχΩ…“‘«σ≥ω![]() ΒΡ ΐ―ßΤΎΆϊ.Θ®2Θ©Θ®iΘ©≈–ΕœΦύΩΊ…ζ≤ζΙΐ≥ΧΒΡΖΫΖ®ΒΡΚœάμ–‘Θ§÷ΊΒψ «ΩΦ¬«“ΜΧλΡΎ≥ι»ΓΒΡ16ΗωΝψΦΰ÷–Θ§≥ωœ÷≥Ώ¥γ‘Ύ
ΒΡ ΐ―ßΤΎΆϊ.Θ®2Θ©Θ®iΘ©≈–ΕœΦύΩΊ…ζ≤ζΙΐ≥ΧΒΡΖΫΖ®ΒΡΚœάμ–‘Θ§÷ΊΒψ «ΩΦ¬«“ΜΧλΡΎ≥ι»ΓΒΡ16ΗωΝψΦΰ÷–Θ§≥ωœ÷≥Ώ¥γ‘Ύ![]() ÷°ΆβΒΡΝψΦΰΒΡΗ≈¬ «¥σΜΙ «–ΓΘ§»τ–ΓΦ¥ΚœάμΘΜΘ®iiΘ©ΗυΨίΧβ…ηΧθΦΰΥψ≥ω
÷°ΆβΒΡΝψΦΰΒΡΗ≈¬ «¥σΜΙ «–ΓΘ§»τ–ΓΦ¥ΚœάμΘΜΘ®iiΘ©ΗυΨίΧβ…ηΧθΦΰΥψ≥ω![]() ΒΡΙάΦΤ÷ΒΚΆ
ΒΡΙάΦΤ÷ΒΚΆ![]() ΒΡΙάΦΤ÷ΒΘ§Χό≥ΐ
ΒΡΙάΦΤ÷ΒΘ§Χό≥ΐ![]() ÷°ΆβΒΡ ΐΨί9.22Θ§Υψ≥ω Θœ¬ ΐΨίΒΡΤΫΨυ ΐΘ§Φ¥ΈΣ
÷°ΆβΒΡ ΐΨί9.22Θ§Υψ≥ω Θœ¬ ΐΨίΒΡΤΫΨυ ΐΘ§Φ¥ΈΣ![]() ΒΡΙάΦΤ÷ΒΘ§Χό≥ΐ
ΒΡΙάΦΤ÷ΒΘ§Χό≥ΐ![]() ÷°ΆβΒΡ ΐΨί9.22Θ§ Θœ¬ ΐΨίΒΡ―υ±ΨΖΫ≤νΘ§Φ¥ΈΣ
÷°ΆβΒΡ ΐΨί9.22Θ§ Θœ¬ ΐΨίΒΡ―υ±ΨΖΫ≤νΘ§Φ¥ΈΣ![]() ΒΡΙάΦΤ÷Β.
ΒΡΙάΦΤ÷Β.
‘ΧβΫβΈωΘΚΘ®1Θ©≥ι»ΓΒΡ“ΜΗωΝψΦΰΒΡ≥Ώ¥γ‘Ύ![]() ÷°ΡΎΒΡΗ≈¬ ΈΣ0.9974Θ§¥”ΕχΝψΦΰΒΡ≥Ώ¥γ‘Ύ
÷°ΡΎΒΡΗ≈¬ ΈΣ0.9974Θ§¥”ΕχΝψΦΰΒΡ≥Ώ¥γ‘Ύ![]() ÷°ΆβΒΡΗ≈¬ ΈΣ0.0026Θ§Ι
÷°ΆβΒΡΗ≈¬ ΈΣ0.0026Θ§Ι ![]() .“ρ¥Υ
.“ρ¥Υ
![]() .
.
![]() ΒΡ ΐ―ßΤΎΆϊΈΣ
ΒΡ ΐ―ßΤΎΆϊΈΣ![]() .
.
Θ®2Θ©Θ®iΘ©»γΙϊ…ζ≤ζΉ¥Χ§’ΐ≥ΘΘ§“ΜΗωΝψΦΰ≥Ώ¥γ‘Ύ![]() ÷°ΆβΒΡΗ≈¬ ÷Μ”–0.0026Θ§“ΜΧλΡΎ≥ι»ΓΒΡ16ΗωΝψΦΰ÷–Θ§≥ωœ÷≥Ώ¥γ‘Ύ
÷°ΆβΒΡΗ≈¬ ÷Μ”–0.0026Θ§“ΜΧλΡΎ≥ι»ΓΒΡ16ΗωΝψΦΰ÷–Θ§≥ωœ÷≥Ώ¥γ‘Ύ![]() ÷°ΆβΒΡΝψΦΰΒΡΗ≈¬ ÷Μ”–0.0408Θ§ΖΔ…ζΒΡΗ≈¬ Κή–Γ.“ρ¥Υ“ΜΒ©ΖΔ…ζ’β÷÷«ιΩωΘ§ΨΆ”–άμ”…»œΈΣ’βΧθ…ζ≤ζœΏ‘Ύ’β“ΜΧλΒΡ…ζ≤ζΙΐ≥Χ―ßΩΤ&ΆχΩ…Ρή≥ωœ÷ΝΥ“λ≥Θ«ιΩωΘ§–ηΕ‘Β±ΧλΒΡ…ζ≤ζΙΐ≥ΧΫχ––Φλ≤ιΘ§Ω…Φϊ…œ ωΦύΩΊ…ζ≤ζΙΐ≥ΧΒΡΖΫΖ® «ΚœάμΒΡ.
÷°ΆβΒΡΝψΦΰΒΡΗ≈¬ ÷Μ”–0.0408Θ§ΖΔ…ζΒΡΗ≈¬ Κή–Γ.“ρ¥Υ“ΜΒ©ΖΔ…ζ’β÷÷«ιΩωΘ§ΨΆ”–άμ”…»œΈΣ’βΧθ…ζ≤ζœΏ‘Ύ’β“ΜΧλΒΡ…ζ≤ζΙΐ≥Χ―ßΩΤ&ΆχΩ…Ρή≥ωœ÷ΝΥ“λ≥Θ«ιΩωΘ§–ηΕ‘Β±ΧλΒΡ…ζ≤ζΙΐ≥ΧΫχ––Φλ≤ιΘ§Ω…Φϊ…œ ωΦύΩΊ…ζ≤ζΙΐ≥ΧΒΡΖΫΖ® «ΚœάμΒΡ.
Θ®iiΘ©”…![]() Θ§ΒΟ
Θ§ΒΟ![]() ΒΡΙάΦΤ÷ΒΈΣ
ΒΡΙάΦΤ÷ΒΈΣ![]() Θ§
Θ§ ![]() ΒΡΙάΦΤ÷ΒΈΣ
ΒΡΙάΦΤ÷ΒΈΣ![]() Θ§”…―υ±Ψ ΐΨίΩ…“‘Ω¥≥ω”–“ΜΗωΝψΦΰΒΡ≥Ώ¥γ‘Ύ
Θ§”…―υ±Ψ ΐΨίΩ…“‘Ω¥≥ω”–“ΜΗωΝψΦΰΒΡ≥Ώ¥γ‘Ύ![]() ÷°ΆβΘ§“ρ¥Υ–ηΕ‘Β±ΧλΒΡ…ζ≤ζΙΐ≥ΧΫχ––Φλ≤ι.
÷°ΆβΘ§“ρ¥Υ–ηΕ‘Β±ΧλΒΡ…ζ≤ζΙΐ≥ΧΫχ––Φλ≤ι.
Χό≥ΐ![]() ÷°ΆβΒΡ ΐΨί9.22Θ§ Θœ¬ ΐΨίΒΡΤΫΨυ ΐΈΣ
÷°ΆβΒΡ ΐΨί9.22Θ§ Θœ¬ ΐΨίΒΡΤΫΨυ ΐΈΣ![]() Θ§“ρ¥Υ
Θ§“ρ¥Υ![]() ΒΡΙάΦΤ÷ΒΈΣ10.02.
ΒΡΙάΦΤ÷ΒΈΣ10.02.
![]() Θ§Χό≥ΐ
Θ§Χό≥ΐ![]() ÷°ΆβΒΡ ΐΨί9.22Θ§ Θœ¬ ΐΨίΒΡ―υ±ΨΖΫ≤νΈΣ
÷°ΆβΒΡ ΐΨί9.22Θ§ Θœ¬ ΐΨίΒΡ―υ±ΨΖΫ≤νΈΣ![]() Θ§
Θ§
“ρ¥Υ![]() ΒΡΙάΦΤ÷ΒΈΣ
ΒΡΙάΦΤ÷ΒΈΣ![]() .
.
ΒψΨΠ: ΐ―ßΤΎΆϊ «άκ…Δ–ΆΥφΜζ±δΝΩ÷–÷Ί“ΣΒΡ ΐ―ßΗ≈ΡνΘ§Ζ¥”≥ΥφΜζ±δΝΩ»Γ÷ΒΒΡΤΫΨυΥ°ΤΫ.«σΫβάκ…Δ–ΆΥφΜζ±δΝΩΒΡΖ÷≤ΦΝ–ΓΔ ΐ―ßΤΎΆϊ ±Θ§ Ήœ»“ΣΖ÷«ε ¬ΦΰΒΡΙΙ≥…”κ–‘÷ Θ§»ΖΕ®άκ…Δ–ΆΥφΜζ±δΝΩΒΡΥυ”–»Γ÷ΒΘ§»ΜΚσΗυΨίΗ≈¬ άύ–Ά―Γ‘ώΙΪ ΫΘ§ΦΤΥψΟΩΗω±δΝΩ»ΓΟΩΗω÷ΒΒΡΗ≈¬ Θ§Ν–≥ωΕ‘”ΠΒΡΖ÷≤ΦΝ–Θ§ΉνΚσ«σ≥ω ΐ―ßΤΎΆϊ.’ΐΧ§Ζ÷≤Φ «“Μ÷÷÷Ί“ΣΒΡΖ÷≤ΦΘ§÷°«ΑΩΦΙΐ“Μ¥ΈΘ§”»Τδ «’ΐΧ§Ζ÷≤ΦΒΡ![]() ‘≠‘ρ.
‘≠‘ρ.

 νΦΌΉς“ΒΚΘ―ύ≥ωΑφ…γœΒΝ–¥πΑΗ
νΦΌΉς“ΒΚΘ―ύ≥ωΑφ…γœΒΝ–¥πΑΗ ±ΨΆΝΫΧΗ®”°‘Ύ νΦΌΗΏ–ßΦΌΤΎΉήΗ¥œΑ‘ΤΡœΩΤΦΦ≥ωΑφ…γœΒΝ–¥πΑΗ
±ΨΆΝΫΧΗ®”°‘Ύ νΦΌΗΏ–ßΦΌΤΎΉήΗ¥œΑ‘ΤΡœΩΤΦΦ≥ωΑφ…γœΒΝ–¥πΑΗ νΦΌΉς“Β±±Ψ©“’ θ”κΩΤ―ßΒγΉ”≥ωΑφ…γœΒΝ–¥πΑΗ
νΦΌΉς“Β±±Ψ©“’ θ”κΩΤ―ßΒγΉ”≥ωΑφ…γœΒΝ–¥πΑΗ