题目内容
【题目】已知函数f(x)=alnx+(x﹣c)|x﹣c|,a<0,c>0 (Ⅰ)当 ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(Ⅱ)设函数f(x)的图象在点P(x1 , f(x1)),Q(x2 , f(x2))两处的切线分别为l1 , l2 . 若 ![]() ,且l1⊥l2 , 求实数c的最小值.
,且l1⊥l2 , 求实数c的最小值.
【答案】解:函数 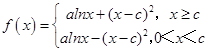 ,求导数
,求导数 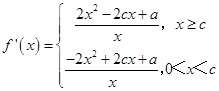 ,
,
(Ⅰ)当 ![]() 时,
时, 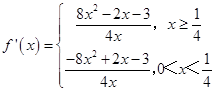 ,
,
若 ![]() ,则
,则 ![]() 恒成立,
恒成立,
所以f(x)在 ![]() 上单调递减;若
上单调递减;若 ![]() ,则
,则 ![]() ,
,
令f'(x)=0,解得 ![]() 或
或 ![]() (舍),
(舍),
当 ![]() 时,f'(x)<0,f(x)在
时,f'(x)<0,f(x)在 ![]() 上单调递减;
上单调递减;
当 ![]() 时,f'(x)>0,f(x)在
时,f'(x)>0,f(x)在 ![]() 上单调递增.
上单调递增.
所以函数f(x)的单调递减区间是 ![]() ,单调递增区间是
,单调递增区间是 ![]()
(Ⅱ)由l1⊥l2知, 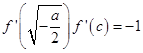 ,而
,而 ![]() ,则
,则 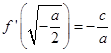 ,
,
若 ![]() ,则
,则 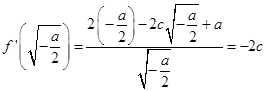
所以 ![]() ,解得
,解得 ![]() ,不符合题意
,不符合题意
故 ![]() ,则
,则 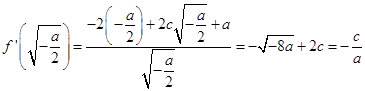
整理得 ![]() ,由c>0,a<0得
,由c>0,a<0得 ![]()
令 ![]() ,则
,则 ![]() ,所以
,所以 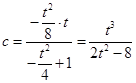
设 ![]() ,当
,当 ![]() 时,g'(t)<0,g(t)在
时,g'(t)<0,g(t)在 ![]() 上单调递减;
上单调递减;
当 ![]() 时,g'(t)>0,g(t)在
时,g'(t)>0,g(t)在 ![]() 上单调递增
上单调递增
所以函数g(t)的最小值为 ![]() ,故实数c的最小值为
,故实数c的最小值为 ![]()
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)根据垂直关系求出a的范围,令 ![]() ,则
,则 ![]() ,表示出c,根据函数的单调性求出c的最小值即可.
,表示出c,根据函数的单调性求出c的最小值即可.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目