Question

【题目】已知直线l在x轴上的截距比在y轴上的截距大1，且过点(6，-2)，求直线l的方程.

Answer 1

【答案】y=-x+2或y=-x+1.

【解析】试题分析：根据题干条件知道过点(6，-2)，可设直线l的点斜式方程为y+2=k(x-6)，分别求出直线的截距，在x轴上的截距比在y轴上的截距大1，故得-(-6k-2)=1，从而求出k值。

方法一：设直线l的点斜式方程为y+2=k(x-6)(k≠0).

令x=0，得y=-6k-2；令y=0，

得x=+6.

于是-(-6k-2)=1，

解得k1=-或k2=-.

故直线l的方程为y+2=- (x-6)或y+2=- (x-6)，即y=-x+2或y=-x+1.

方法二：设直线l的斜截式方程为y=kx+b.

令y=0，得x=-.

依题意，得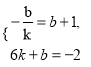

或

故直线l的方程为y=-x+1或y=-x+2.