题目内容
已知抛物线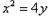 ,过点
,过点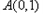 任意作一条直线
任意作一条直线 交抛物线
交抛物线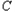 于
于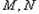 两点,
两点,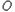 为坐标原点.
为坐标原点.
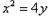 ,过点
,过点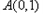 任意作一条直线
任意作一条直线 交抛物线
交抛物线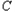 于
于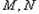 两点,
两点,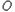 为坐标原点.
为坐标原点.(1)求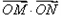 的值;
的值;
(2)过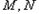 分别作抛物线
分别作抛物线 的切线
的切线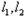 ,试探求
,试探求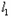 与
与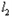 的交点是否在定直线上,并证明你的结论.
的交点是否在定直线上,并证明你的结论.
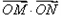 的值;
的值;(2)过
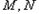 分别作抛物线
分别作抛物线 的切线
的切线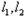 ,试探求
,试探求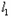 与
与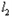 的交点是否在定直线上,并证明你的结论.
的交点是否在定直线上,并证明你的结论.解:(Ι)设直线 方程为
方程为 ,
,
 消去
消去 得
得 ,
,
所以
 =
=
故 .
.
(Π)
 方程为
方程为
整理得
同理得 方程为
方程为 ;
;
联立方程
 得
得 ,
,
故 的交点的纵坐标等于
的交点的纵坐标等于 .
.
 方程为
方程为 ,
,
 消去
消去 得
得 ,
,所以

 =
=
故
 .
. (Π)

 方程为
方程为
整理得

同理得
 方程为
方程为 ;
;联立方程

 得
得 ,
,
故
 的交点的纵坐标等于
的交点的纵坐标等于 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,点
,点 为其焦点,点
为其焦点,点 在抛物线
在抛物线 的内部,设点
的内部,设点 是抛物线
是抛物线 的最小值为4.
的最小值为4. 与抛物线
与抛物线 、
、 ,与
,与 轴交于点
轴交于点 ,且
,且 ,试判断
,试判断 是否为定值?若是定值,求出该定值并证明;若不是定值,
是否为定值?若是定值,求出该定值并证明;若不是定值,