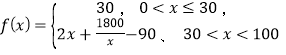题目内容
【题目】已知![]() 是曲线
是曲线![]() 上动点以及定点
上动点以及定点![]() ,
,![]()
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求![]() 面积的最小值,并求出相应的点的坐标.
面积的最小值,并求出相应的点的坐标.
【答案】(1) ![]() ;(2)
;(2) ![]() 的面积最小值为1,此时点
的面积最小值为1,此时点![]() 坐标为
坐标为![]() .
.
【解析】
(1)求得导函数,根据导数的几何意义,即可求得斜率和切点坐标,根据点斜式即可写出切线方程;
(2)由![]() 坐标即可求得直线
坐标即可求得直线![]() 方程, 当点P为与
方程, 当点P为与![]() 平行且且与曲线
平行且且与曲线![]() 相切的直线的切点时,
相切的直线的切点时, ![]() 面积的最小值,根据导数的几何意义即可求得切点,利用点到直线距离公式即可求得P到AB的距离,进而求得面积.
面积的最小值,根据导数的几何意义即可求得切点,利用点到直线距离公式即可求得P到AB的距离,进而求得面积.
解: ![]() ,
,![]() ,
,![]() .
.
(1)当![]() ,
,![]() ,
,![]() ,即切点为
,即切点为![]() ,切线方程为
,切线方程为![]() ,化简得:
,化简得: ![]() .
.
(2)直线![]() 的方程为:
的方程为:![]() ,设与
,设与![]() 平行且与曲线
平行且与曲线![]() 相切的直线为
相切的直线为![]() 即
即![]() ,解得:
,解得:![]() ,则切点为
,则切点为![]() ,即点
,即点![]() 坐标为
坐标为![]() 时,
时, ![]() 的面积最小,
的面积最小,![]() ,
, ![]() 到直线
到直线![]() :
:![]() 的距离为
的距离为![]() ,所以
,所以![]() .
.

练习册系列答案
相关题目