题目内容

函数f（x）=x•2^x取得极值时的x的值为________．

-log₂e
分析：直接根据常用函数的导函数以及求导法则求其导函数，找到导函数为0的根即可得出结论．
解答：∵f′（x）=2^x+x•2^x•ln2=0
即2^x（1+x•ln2）=0
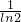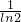解得：x=- $\text{[math]}$ =-log2^e．
故答案为：-log2^e．
点评：解决此类问题的关键是熟悉导数的作用即判断单调性，求极值，求切线方程等，解题时要正确利用公式求函数的导数．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

设函数f（x）=a²x²（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为

，求a的值；
（2）关于x的不等式（x-1）²＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=

，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

（2012•深圳一模）已知函数f(x)=

x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x

， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．

（2011•上海模拟）已知函数f(x)=(

-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2^m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k²，b=（k+c）²时，记f（x）=f₁（x）；当a=（k+c）²，b=（k+2c）²时，记f（x）=f₂（x）．
求证：f1(x)+f2(x)＞

已知函数f(x)=(

-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2^m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k²，b=（k+c）²时，记f（x）=f₁（x）；当a=（k+c）²，b=（k+2c）²时，记f（x）=f₂（x）．
求证：f1(x)+f2(x)＞

设函数f（x）=a²x²（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2

，求a的值；
（2）关于x的不等式（x-1）²＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=

，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．