题目内容
某研究性学习小组要制作一个容积为0.18m3，深为0.5m的长方体无盖水箱，箱底和箱壁的造价每平方米分别为400元和100元，那么水箱的最低总造价为
264
264
元．分析：分别确定箱底和箱壁的造价，利用基本不等式，可求最值．
解答：解：设池底一边为x米，则另一边为
米，
总造价为y元，则y=100×0.5×(2x+
)+0.36×400=100（x+
）+144≥264，
当且仅当x=
，即x=0.6米时，ymin=264元．
故答案为：264．
| 0.36 |
| x |
总造价为y元，则y=100×0.5×(2x+
| 0.72 |
| x |
| 0.36 |
| x |
当且仅当x=
| 0.36 |
| x |
故答案为：264．
点评：本题考查利用数学知识解决实际问题，考查基本不等式的运用，确定函数解析式是关键．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
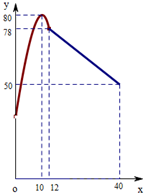学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数y与听课时间x（单位：分钟）之间的关系满足如图所示的图象，当x∈（0，12]时，图象是二次函数图象的一部分，其中顶点A（10，80），过点B（12，78）；当x∈[12，40]时，图象是线段BC，其中C（40，50）．根据专家研究，当注意力指数大于62时，学习效果最佳．