题目内容
18.在平面直角坐标系xOy中,曲线C的参数方程为$\left\{\begin{array}{l}{x=a+acosβ}\\{y=asinβ}\end{array}\right.$(a>0,β为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程ρcos(θ-$\frac{π}{3}$)=$\frac{3}{2}$.(Ⅰ)若曲线C与l只有一个公共点,求a的值;
(Ⅱ)A,B为曲线C上的两点,且∠AOB=$\frac{π}{3}$,求△OAB的面积最大值.
分析 (Ⅰ)根据sin2β+cos2β=1消去β为参数可得曲线C的普通方程,根据ρcosθ=x,ρsinθ=y,ρ2=x2+y2,直线l的极坐标方程化为普通方程,曲线C与l只有一个公共点,即圆心到直线的距离等于半径,可得a的值.
(Ⅱ)利用极坐标方程的几何意义求解即可.
解答 (Ⅰ)曲线C是以(a,0)为圆心,以a为半径的圆;
直线l的直角坐标方程为$x+\sqrt{3}y-3=0$
由直线l与圆C只有一个公共点,则可得$\frac{|a-3|}{2}=a$
解得:a=-3(舍)或a=1
所以:a=1.
(Ⅱ)由题意,曲线C的极坐标方程为ρ=2acosθ(a>0)
设A的极角为θ,B的极角为$θ+\frac{π}{3}$
则:${S}_{△OAB}=\frac{1}{2}|OB|•|OA|Sin\frac{π}{3}$=$\frac{\sqrt{3}}{4}|2acosθ|•|2acos(θ+\frac{π}{3})|$=$\sqrt{3}{a}^{2}|cosθ•cos(θ+\frac{π}{3})|$
∵cos$θ•cos(θ+\frac{π}{3})$=$\frac{1}{2}cos(2θ+\frac{π}{3})+\frac{1}{4}$
所以当$θ=-\frac{π}{6}$时,$\frac{1}{2}cos(2θ+\frac{π}{3})+\frac{1}{4}$取得最大值$\frac{3}{4}$
∴△OAB的面积最大值为$\frac{3\sqrt{3}{a}^{2}}{4}$.
解法二:因为曲线C是以(a,0)为圆心,以a为半径的圆,且$∠AOB=\frac{π}{3}$
由正弦定理得:$\frac{|AB|}{sin\frac{π}{3}}=2a$,所以|AB=$\sqrt{3}a$
由余弦定理得:|AB2=3a2=|0A|2+|OB|2-|OA||OB|≥|OA||OB|
则:${S}_{△OAB}=\frac{1}{2}|OB|•|OA|Sin\frac{π}{3}$≤$\frac{1}{2}$×$3{a}^{2}×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}{a}^{2}}{4}$.
∴△OAB的面积最大值为$\frac{3\sqrt{3}{a}^{2}}{4}$.
点评 本题考查参数方程、极坐标方程、普通方程的互化,以及应用,属于中档题

| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | 10步、50步 | B. | 20步、60步 | C. | 30步、70步 | D. | 40步、80步 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{7}{6}$ | B. | 1 | C. | $\frac{3}{4}$ | D. | $\frac{8}{9}$ |
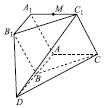 如图,已知平面ADC∥平面A1B1C1,B为线段AD的中点,△ABC≈△A1B1C1,四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1,A1C1=A1A,∠C1A1A=$\frac{π}{3}$,M为棱A1C1的中点.
如图,已知平面ADC∥平面A1B1C1,B为线段AD的中点,△ABC≈△A1B1C1,四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1,A1C1=A1A,∠C1A1A=$\frac{π}{3}$,M为棱A1C1的中点.