题目内容
函数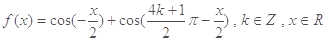 .
.
(1)求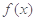 的周期;
的周期;
(2)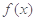 在
在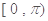 上的减区间;
上的减区间;
(3)若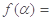
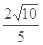 ,
,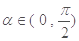 ,求
,求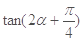 的值.
的值.
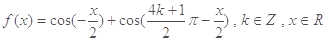 .
.(1)求
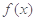 的周期;
的周期;(2)
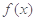 在
在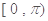 上的减区间;
上的减区间; (3)若
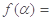
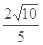 ,
,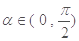 ,求
,求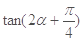 的值.
的值.(1) ;(2)
;(2)  ;(3)
;(3)  .
.
 ;(2)
;(2)  ;(3)
;(3)  .
.试题分析:(1)先利用三角函数的诱导公式将函数
 化为
化为 形式,再利用辅助角公式将其化为
形式,再利用辅助角公式将其化为 的形式,则周期公式
的形式,则周期公式 可求得周期.
可求得周期.(2)先将
 看成一个整体,由
看成一个整体,由 解得正弦函数的减区间,再取
解得正弦函数的减区间,再取 值,可求得函数
值,可求得函数 在
在 上的减区间.
上的减区间.(3)将
 代入(1)中的解析式可求得
代入(1)中的解析式可求得 的值,又因为
的值,又因为 ,根据同角三角函数的基本关系式
,根据同角三角函数的基本关系式 、
、 可求得
可求得 、
、 的值,再根据两角和的正切公式
的值,再根据两角和的正切公式 、二倍角公式
、二倍角公式 可求得
可求得 .
.试题解析:(1)

 ,(
,( ), 所以
), 所以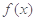 的周期
的周期 .
.(2)由
 ,得
,得 .
.又
 ,令
,令 ,得
,得
 ;令
;令 ,得
,得 (舍去)
(舍去) ∴
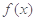 在
在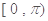 上的减区间是
上的减区间是 .
. (3)由
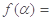
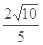 ,得
,得 ,∴
,∴  , ∴
, ∴
又
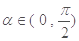 ,∴
,∴
∴
 ,∴
,∴
∴
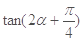
 .
.
练习册系列答案
相关题目
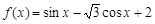 ,记函数
,记函数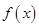 的最小正周期为
的最小正周期为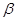 ,向量
,向量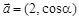 ,
,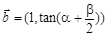 (
(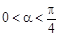 ),且
),且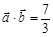 .
.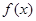 在区间
在区间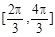 上的最值;
上的最值;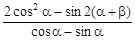 的值.
的值.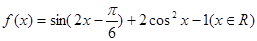
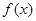 的单调递增区间;
的单调递增区间;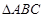 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为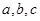 ,已知
,已知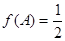 ,
,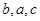 成等差数列,且
成等差数列,且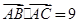 ,求边
,求边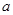 的值.
的值.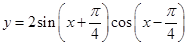 和直线
和直线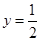 在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3…,则|P2P4|等于______________。
在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3…,则|P2P4|等于______________。 满足
满足 ,则称
,则称 ; ②
; ② ;
;
 是
是 的内角).
的内角).



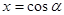 ,
,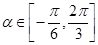 ,则
,则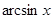 的取值范围为___________.
的取值范围为___________.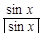 +
+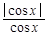 +
+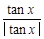 的值域是( )
的值域是( ) 的最小值和最大值分别为( )
的最小值和最大值分别为( ) 3,1
3,1
 )-sin2(x-
)-sin2(x- (
( ,
, )的值域是_______。
)的值域是_______。