题目内容
等腰梯形ABCD,上底边CD=1,腰AD=CB=
,下底AB=3,按平行于上、下底边取x轴,则直观图A′B′C′D′的面积为
______.
| 2 |
等腰梯形ABCD,上底边CD=1,腰AD=CB=
,下底AB=3,所以梯形的高为:1,
按平行于上、下底边取x轴,则直观图A′B′C′D′的高为:
sin45°=
所以直观图的面积为:
×(1+3)×
=
故答案为:
| 2 |
按平行于上、下底边取x轴,则直观图A′B′C′D′的高为:
| 1 |
| 2 |
| ||
| 4 |
所以直观图的面积为:
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
故答案为:
| ||
| 2 |

练习册系列答案
相关题目


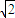 ,下底AB=3,按平行于上、下底边取x轴,则直观图A′B′C′D′的面积为 .
,下底AB=3,按平行于上、下底边取x轴,则直观图A′B′C′D′的面积为 .