题目内容
等腰梯形ABCD，上底边CD=1，腰AD=CB=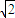
，下底AB=3，按平行于上、下底边取x轴，则直观图A′B′C′D′的面积为 ．
【答案】分析：根据题意求出直观图A′B′C′D′的高，利用梯形的面积公式求解即可．
解答：解：等腰梯形ABCD，上底边CD=1，腰AD=CB=
，下底AB=3，所以梯形的高为：1，
按平行于上、下底边取x轴，则直观图A′B′C′D′的高为：
所以直观图的面积为：
=
故答案为：
点评：本题考查空间图形的直观图的画法，考查计算能力，注意：直观图的高是平面图形高的
倍，此处容易出错．
解答：解：等腰梯形ABCD，上底边CD=1，腰AD=CB=
，下底AB=3，所以梯形的高为：1，按平行于上、下底边取x轴，则直观图A′B′C′D′的高为：
所以直观图的面积为：
=故答案为：
点评：本题考查空间图形的直观图的画法，考查计算能力，注意：直观图的高是平面图形高的
倍，此处容易出错． 
练习册系列答案
相关题目
