题目内容
设U={(x,y)|x2+y2≤1,x,y∈R},M={(x,y)|x|+|y|≤1,x,y∈R},现有一质点随机落入区域U中,则质点落入M中的概率是
- A.
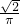
- B.

- C.
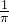
- D.

D
分析:本题考查的知识点是几何根据,根据U={(x,y)|x2+y2≤1,x,y∈R},我们计算出满足条件的平面图形的面积,再由计算满足条件M={(x,y)|x|+|y|≤1,x,y∈R}的面积,代入几何概型计算公式,即可得到答案.
解答: 解:满足条件U={(x,y)|x2+y2≤1,x,y∈R}的圆,如下图示:
解:满足条件U={(x,y)|x2+y2≤1,x,y∈R}的圆,如下图示:
其中满足条件M={(x,y)|x|+|y|≤1,x,y∈R}的平面区域如图中阴影所示:
则圆的面积S圆=π
阴影部分的面积S阴影=2
故质点落入M中的概率概率P= =
=
故选D
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=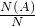 求解.
求解.
分析:本题考查的知识点是几何根据,根据U={(x,y)|x2+y2≤1,x,y∈R},我们计算出满足条件的平面图形的面积,再由计算满足条件M={(x,y)|x|+|y|≤1,x,y∈R}的面积,代入几何概型计算公式,即可得到答案.
解答:
 解:满足条件U={(x,y)|x2+y2≤1,x,y∈R}的圆,如下图示:
解:满足条件U={(x,y)|x2+y2≤1,x,y∈R}的圆,如下图示:其中满足条件M={(x,y)|x|+|y|≤1,x,y∈R}的平面区域如图中阴影所示:
则圆的面积S圆=π
阴影部分的面积S阴影=2
故质点落入M中的概率概率P=
 =
=
故选D
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
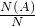 求解.
求解. 
练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
设U=R,集合A={y|y=
,x≥1},B={x∈Z|x2-4≤0},则下列结论正确的是( )
| x-1 |
| A、A∩B={-2,-1} |
| B、(?UA)∪B=(-∞,0) |
| C、A∪B=[0,+∞) |
| D、(?UA)∩B={-2,-1} |

