题目内容
在△ABC中，AC=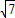
，BC=2，B=60°则BC边上的高等于（ ）A．
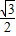
B．
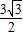
C．
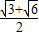
D．
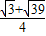
【答案】分析：在△ABC中，由余弦定理可得，AC2=AB2+BC2-2AB•BCcosB可求AB=3，作AD⊥BC，则在Rt△ABD中，AD=AB×sinB
解答：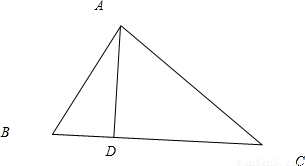
解：在△ABC中，由余弦定理可得，AC2=AB2+BC2-2AB•BCcosB
把已知AC=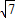
，BC=2 B=60°代入可得，7=AB2+4-4AB×
整理可得，AB2-2AB-3=0
∴AB=3
作AD⊥BC垂足为D
Rt△ABD中，AD=AB×sin60°=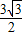
，
即BC边上的高为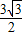
故选B
点评：本题主要考查了余弦定理在解三角形中的应用，解答本题的关键是求出AB，属于基础试题
解答：
解：在△ABC中，由余弦定理可得，AC2=AB2+BC2-2AB•BCcosB把已知AC=
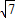，BC=2 B=60°代入可得，7=AB2+4-4AB×整理可得，AB2-2AB-3=0
∴AB=3
作AD⊥BC垂足为D
Rt△ABD中，AD=AB×sin60°=
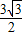，即BC边上的高为
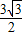
故选B
点评：本题主要考查了余弦定理在解三角形中的应用，解答本题的关键是求出AB，属于基础试题
练习册系列答案
金钥匙试卷系列答案
相关题目
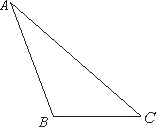如图，在△ABC中，AC=2，BC=1，
如图，在△ABC中，AC=BC，AB=2，O为AB的中点，沿OC将△AOC折起到△A′OC的位置，使得直线A′B与平面ABC成30°角．