题目内容
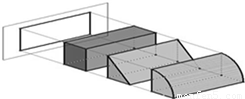如图，三个几何体，一个是长方体、一个是直三棱柱，一个是过圆柱上下底面圆心切下圆柱的四分之一部分，这三个几何体的主视图和俯视图是相同的正方形，则它们的体积之比为 ．
【答案】分析：利用三视图判断三个几何体的特征，设出正方体的棱长，分别求出几何体的体积，即可得到比值．
解答：解：因为三个几何体的主视图和俯视图为相同的正方形，所以原长方体棱长相等为正方体，
原直三棱柱是底面为等腰直角三角形的直三棱柱，
设正方体的棱长为1，
则长方体体积为：1，
三棱柱体积为：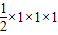
=
，
四分之一圆柱的体积为：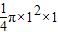
=
，
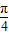所以它们的体积之比为4：2：π
故答案为：4：2：π．
点评：本题考查几何体与三视图的关系，几何体的体积的求法，考查计算能力．
解答：解：因为三个几何体的主视图和俯视图为相同的正方形，所以原长方体棱长相等为正方体，
原直三棱柱是底面为等腰直角三角形的直三棱柱，
设正方体的棱长为1，
则长方体体积为：1，
三棱柱体积为：
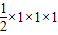=，四分之一圆柱的体积为：
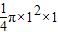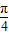=，所以它们的体积之比为4：2：π
故答案为：4：2：π．
点评：本题考查几何体与三视图的关系，几何体的体积的求法，考查计算能力．
练习册系列答案
相关题目
求答下列三小题：
已知一几何体的三视图如图，正视图和侧视图都是矩形，俯视图为正方形，在该几何体上任意选择5个顶点，它们可能是如下各种几何形体的5个顶点，这些几何形体是（写出所有正确结论的编号）
已知一几何体的三视图如图，主视图和左视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，以这4个点为顶点的几何形体可能是（ ）
如图所示，在三棱柱A1B1C1-ABC中，AA1⊥底面ABC，AC⊥BC．AC=BC=CC1=2．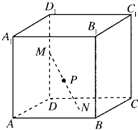
如图，已知正方体ABCD-A1B1C1D1的棱长为a（a＞2），长度为2的线段MN的一个端点M在DD1上运动，另一端点N在底面ABCD上运动，则MN的中点P的轨迹（曲面）与共一顶点D的三个面所围成的几何体的体积为