题目内容
等边三角形ABC中，P在线段AB上，且
=λ
，若
•
=
•
，则实数λ的值是
．
| AP |
| AB |
| CP |
| AB |
| PA |
| PB |
2-
| ||
| 2 |
2-
| ||
| 2 |
分析：将
表示为
+
，利用向量数量积公式，将关系式化简得出关于λ的方程并解出即可．注意0＜λ＜1．
| CP |
| CA |
| AP |
解答：解：设等边三角形ABC的边长为1．则|
|=λ|
=λ，
|=1-λ．（0＜λ＜1）
•
=(
+
)•
=
•
+
•
=
•
，
所以
1×1×cos120°+λ×1×cos0°=λ×（1-λ）cos180°．
化简-
+λ=-λ（1-λ），整理λ2-2λ+
=0，解得λ=
（λ=
＞1舍去）
故答案为：
| AP |
| AB| |
| |PB |
| CP |
| AB |
| CA |
| AP |
| AB |
| CA |
| AB |
| AP |
| AB |
| PA |
| PB |
所以
1×1×cos120°+λ×1×cos0°=λ×（1-λ）cos180°．
化简-
| 1 |
| 2 |
| 1 |
| 2 |
2-
| ||
| 2 |
2+
| ||
| 2 |
故答案为：
2-
| ||
| 2 |
点评：本题考查向量数量积的运算，平面向量基本定理，关键是将
表示为
+
，进行转化，以便应用向量数量积公式计算化简．
| CP |
| CA |
| AP |
练习册系列答案
相关题目
在边长为a的等边三角形ABC中，AD⊥BC于D，沿AD折成二面角B-AD-C后，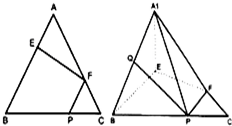
（2013•汕头二模）如图，在边长为3的等边三角形ABC中，E，F，P分别为AB，AC，BC边上的点，且满足AE=FC=CP=1，将△AEF沿EF折起到△A1EF的位置，如图，使平面A1EF⊥平面FEBP，连结A1B，A1P，